coin flip probability experiment

January 1, 2024

Scientists Destroy Illusion That Coin Toss Flips Are 50–50

Researchers go to great lengths to prove a tiny bias in coin flipping

By Shi En Kim

Thomas Fuchs

Join Our Community of Science Lovers!

The phrase “ coin toss ” is a classic synonym for randomness. But since at least the 18th century, mathematicians have suspected that even fair coins tend to land on one side slightly more often than the other. Proving this tiny bias, however, would require hundreds of thousands of meticulously recorded coin flips, making laboratory tests a logistical nightmare.

František Bartoš, currently a Ph.D. candidate studying the research methods of psychology at the University of Amsterdam, became intrigued by this challenge four years ago. He couldn't round up enough volunteers to investigate it at first. “Nobody was stupid enough to spend a couple of weekends flipping coins,” he says. But after he began his Ph.D. studies, he tried again, recruiting 47 volunteers (many of them friends and fellow students) from six countries. Multiple weekends of coin flipping later, including one 12-hour marathon session , the team had performed 350,757 tosses, shattering the previous record of 40,000.

The flipped coins, according to findings in a preprint study posted on arXiv.org , landed with the same side facing upward as before the toss 50.8 percent of the time. The large number of throws allows statisticians to conclude that the nearly 1 percent bias isn't a fluke. “We can be quite sure there is a bias in coin flips after this data set,” Bartoš says.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

The leading theory explaining the subtle advantage comes from a 2007 physics study by Stanford University statistician Persi Diaconis and his colleagues, whose calculations predicted a same-side bias of 51 percent. From the moment a coin is launched into the air, its entire trajectory—including whether it lands on heads or tails—can be calculated by the laws of mechanics. The researchers determined that airborne coins don't turn around their symmetrical axis; instead they tend to wobble off-center, which causes them to spend a little more time aloft with their initial “up” side on top.

For day-to-day decisions, coin tosses are as good as random because a 1 percent bias isn't perceptible with just a few coin flips, says statistician Amelia McNamara of the University of St. Thomas in Minnesota, who wasn't involved in the new research. Still, the study's conclusions should dispel any lingering doubt regarding the coin flip's slender bias. “This is great empirical evidence backing that up,” she says.

It isn't difficult to prevent this bias from influencing your coin-toss matches; simply concealing the coin's starting position before flipping it should do the trick. Alternatively, you can do away with flipping altogether by jiggling a coin between your curved palms. But if your friends are unaware of the tiny bias, you may as well benefit from your slight advantage. After all, 51 percent odds beat a casino's house advantage for six-deck blackjack. “If you asked me to bet on a coin,” Bartoš says, “why wouldn't I give myself a 1 percent bias?”

Advertisement

Mathematics

Coin flips don't truly have a 50/50 chance of being heads or tails.

Researchers who flipped coins 350,757 times have confirmed that the chance of landing the coin the same way up as it started is around 51 per cent

By Matthew Sparkes

17 October 2023

Place your bets

Image Source Trading Ltd/Shutterstock

If you flip a coin, the odds of getting heads or tails are an equal 50 per cent chance – right? While this is what statistics textbooks will tell you, there is increasing evidence that it isn’t quite true in the real world.

In 2007, researchers theorised that when a coin is flipped, the flipper’s thumb imparts a slight wobble to it, causing it to spend more time with one side facing upwards while in the air and making it more likely to land showing that side. They predicted that a coin should land showing the same side that was facing up when flipped approximately 51 per cent of the time.

Now, František Bartoš at the University of Amsterdam in the Netherlands and a team of 49 others have conducted the most robust test of this theory yet carried out. He recruited dozens of friends and colleagues for a marathon coin-flipping session.

“When you and your friends sit in a room, play some music, chat, it’s like a nice activity,” he says. “Some people watch movies together and some people flip coins for 12 hours. It’s actually much more pleasant than you would expect.”

The team tossed coins of 46 different currencies and denominations 350,757 times and recorded both the pre-flipping and post-flipping state. The findings backed up the original research: coins are likely to land on the same side they started on 50.8 per cent of the time.

Crucially, though, the team found large variations in flippers. One person landed coins on the same side they started on 60.1 per cent of the time, while one at the other end of the spectrum landed their coins in this way just 48.7 per cent of the time. The researchers say that different people may impart more off-axis rotation when they flip a coin, causing it to wobble and creating a higher same-side bias.

Sign up to our The Daily newsletter

The latest science news delivered to your inbox, every day.

Márton Balázs at the University of Bristol, UK, who wasn’t involved in the research, says that coin flips in probability terms are an abstract idea, but that actually flipping a coin “is a complicated physical, psychological process”.

“An ideal coin is an abstraction. There is no such thing as an ideal coin,” he says. “It’s a complicated process. So there is a skew. It seems to be relatively small skew, like a few per cent, but it’s still there.”

Mathematicians find 27 tickets that guarantee UK National Lottery win

Balázs says that anyone looking for a truly random result should avoid coins, but that even turning to a computer won’t be truly random, as they are notoriously unable to generate random results without repeating patterns. Anyone looking for true randomness would have to rely on sampling chaotic systems such as the weather or the motion of blobs in lava lamps , he says.

Bartoš says that although the findings show coin flips have a bias, they can still be used for everyday decisions – as long as both parties don’t see the starting state of the coin before the flip.

arXiv DOI: 10.48550/arXiv.2310.04153

Sign up to our weekly newsletter

Receive a weekly dose of discovery in your inbox! We'll also keep you up to date with New Scientist events and special offers.

More from New Scientist

Explore the latest news, articles and features

Ancient Egyptians shaped sheep's horns – and we don't know why

Subscriber-only

Knots made in a weird quantum fluid can last forever

Tom Gauld on getting things to work - or not

Twisteddoodles on (another) new method for teaching mathematics

Popular articles.

Trending New Scientist articles

Coin Flip Probability Calculator

Table of contents

Welcome to the coin flip probability calculator , where you'll have the opportunity to learn how to calculate the probability of obtaining a set number of heads (or tails) from a set number of tosses. This is one of the fundamental classical probability problems, which later developed into quite a big topic of interest in mathematics.

For example, maybe you like Batman and know of one of his many villains, Two-Face? You'd think that his name comes from the fact that half of his face is burnt, but no! (Okay, maybe a little bit.) He has a lucky coin that he always flips before doing anything. As this coin has two faces on it, his coin toss probability of getting a head is 1. Better not get on the wrong side (or face) of him!

🙋 If you're interested in the probability of runs in coin flips, visit our dedicated coin toss streak calculator .

Classical probability

The probability of some event happening is a mathematical (numerical) representation of how likely it is to happen , where a probability of 1 means that an event will always happen, while a probability of 0 means that it will never happen. Classical probability problems often need you to find how often one outcome occurs versus another and how one event happening affects the probability of future events happening. When you look at all the things that may occur, the formula (just as our coin flip probability formula ) states that:

probability = (no. of successful results) / (no. of all possible results) .

Take a die roll as an example . If you have a standard, 6-face die, then there are six possible outcomes, namely the numbers from 1 to 6. If it is a fair die, then the likelihood of each of these results is the same , i.e., 1 in 6 or 1 / 6 . Therefore, the probability of obtaining 6 when you roll the die is 1 / 6 . The probability is the same for 3. Or 2. You get the drill. If you don't believe me, take a die and roll it a few times, and note the results. Remember that the more times you repeat an experiment, the more trustworthy the results . So go on, roll it, say, a thousand times. We'll be waiting here until you get back to tell us we've been right all along. Go to the dice probability calculator if you want a shortcut.

But what if you repeat an experiment a hundred times and want to find the odds that you'll obtain a fixed result at least 20 times?

Let's look at another example. Say that you're a teenager straight out of middle school and decide that you want to meet the love of your life this year. More specifically, you want to ask ten girls out and go on a date with only four of them. One of those has got to be the one, right? The first thing you have to do in this situation is look in the mirror and rate how likely a girl is to agree to go out with you when you start talking to her. If you have problems with assessing your looks fairly, go downstairs and let your grandma tell you what a handsome young gentleman you are . So a solid 9 / 10 then.

As you only want to go on four dates, that means you only want four of your romance attempts to succeed. This has an outcome of 9 / 10 . This means that you want the other six girls to reject you, which, based on your good looks, has only a 1 / 10 chance of happening (The sum of all events happening is always equal to 1, so we get this number by subtracting 9 / 10 from 1). If you multiply the probability of each event by the number of times you want it to occur, you get the chance that your scenario will come true. In this case, your odds are 210 × (9 / 10) 4 × (1 / 10) 6 = 0.000137781 , where the 210 comes from the number of possible fours of girls among the ten that would agree. Not very likely to happen, is it? Maybe you should try being less beautiful!

How to calculate probability?

" Hey man, but girls and coins are two different things! I should know; I've seen at least one of each. " Well, let me explain that these two problems are basically the same , that is, from the point of view of mathematics. Whether you want to toss a coin or ask a girl out, there are only two possibilities that can occur. In other words, if you assign the success of your experiment, be it getting tails or the girl agreeing to your proposal, to one side of the coin and the other option to the back of the coin, the coin toss probability will determine the answer . It all boils down to getting your hands on a coin that is weighted appropriately. Mathematically, we talk about the binomial probability distribution .

Let's look at a step-by-step example to see how to calculate the probability of an event using the coin toss probability calculator:

Determine your experiment. What are the two possibilities that can happen? Assign heads to one of them and tails to the other.

How many times are you going to repeat the experiment? Put that number as the number of flips in the calculator.

What do you want to achieve? An exact number of successful tries? At least a set number of successful attempts? Or no more than a certain number of successful tries? Choose the correct option from the list.

How many successful (exact, at least, or at most) attempts do you want to have? Input that number of heads .

(Optional) If your heads and tails don't have the same probability of happening, set the right number in the Probability of heads field. Remember that in classical probability, the likelihood cannot be smaller than 0 or larger than 1.

The coin flip probability calculator will automatically calculate the chance of your event happening .

More complex probabilities

You know how they say that money can't buy you happiness? Well, it's true that there are times when a coin is not enough if you want to count the likelihood of something happening. If your problem still falls under the umbrella of classical probability – meaning you can determine how many successful results there exist and how many possibilities there are in general – then the coin flip probability formula from the first section will work just fine.

If you are looking for your chances of winning the lottery or surviving on a desert island, then things start to get more complicated than a simple coin toss probability. (The former is, in fact, covered in Omni's lottery calculator .)

What is the formula for the probability in coin toss?

If you flip a fair coin n times, the probability of getting exactly k heads is P(X=k) = (n choose k)/2 n , where:

• (n choose k) = n! / (k! × (n-k)!) ; and
• ! is the factorial , that is, n! stands for the multiplication 1 × 2 × 3 × ... (n-1) × n.

How do I compute the probability of 8 heads in 10 tosses?

To calculate the probability of 8 heads in 10 tosses:

• Recall the formula for the probability of exactly k heads in n tosses: P(X=k) = (n choose k)/2 n .
• Thus, the probability of exactly 8 heads in 10 tosses is P(X=8) = (10 choose 8)/2 10 = 45/1024 ≈ 0.044.
• If you need the probability of at least 8 heads , find P(X=8) + P(X=9) + P(X=10) .
• We have P(X=9) = 10/1024 ≈ 0.0098 and P(X=10) = 1/1024 ≈ 0.001.
• The answer is 0.044 + 0.0098 + 0.001 ≈ 0.0548 .

What is the probability of 2 heads in 3 tosses?

If you toss a coin 3 times, the probability of at least 2 heads is 50% , while that of exactly 2 heads is 37.5% . Here's the sample space of 3 flips: {HHH, THH, HTH, HHT, HTT, THT, TTH, TTT​} . There are 8 possible outcomes. Three contain exactly two heads, so P(exactly two heads) = 3/8=37.5%. One outcome contains three heads, so P(at least two heads) = (3+1)/8 = 50%.

What is the probability of at least 1 head in 4 tosses?

The probability of at least 1 head in 4 tosses is 93.75%. To see why, observe that we have P(at least 1 heads) = 1 - P(no heads) = 1 - P(all tails) and P(all tails) = (1/2) 4 = 0.0625 . Therefore, P(at least 1 heads) = 1 - 0.0625 = 0.9375 = 93.75% , as claimed.

.css-m482sy.css-m482sy{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-m482sy.css-m482sy:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-m482sy .js-external-link-button.link-like,.css-m482sy .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-m482sy .js-external-link-button.link-like:hover,.css-m482sy .js-external-link-anchor:hover,.css-m482sy .js-external-link-button.link-like:active,.css-m482sy .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-m482sy .js-external-link-button.link-like:focus-visible,.css-m482sy .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-m482sy p,.css-m482sy div{margin:0;display:block;}.css-m482sy pre{margin:0;display:block;}.css-m482sy pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-m482sy pre:not(:first-child){padding-top:8px;}.css-m482sy ul,.css-m482sy ol{display:block margin:0;padding-left:20px;}.css-m482sy ul li,.css-m482sy ol li{padding-top:8px;}.css-m482sy ul ul,.css-m482sy ol ul,.css-m482sy ul ol,.css-m482sy ol ol{padding-top:0;}.css-m482sy ul:not(:first-child),.css-m482sy ol:not(:first-child){padding-top:4px;} .css-1d24qkw{margin:auto;overflow:auto;overflow-wrap:break-word;word-break:break-word;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-1d24qkw .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-1d24qkw .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-1d24qkw .katex .katex-version::after{content:'0.13.13';}.css-1d24qkw .katex .katex-mathml{position:absolute;clip:rect(1px,1px,1px,1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-1d24qkw .katex .katex-html>.newline{display:block;}.css-1d24qkw .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-1d24qkw .katex .strut{display:inline-block;}.css-1d24qkw .katex .textbf{font-weight:bold;}.css-1d24qkw .katex .textit{font-style:italic;}.css-1d24qkw .katex .textrm{font-family:KaTeX_Main;}.css-1d24qkw .katex .textsf{font-family:KaTeX_SansSerif;}.css-1d24qkw .katex .texttt{font-family:KaTeX_Typewriter;}.css-1d24qkw .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-1d24qkw .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-1d24qkw .katex .mathrm{font-style:normal;}.css-1d24qkw .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-1d24qkw .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-1d24qkw .katex .amsrm{font-family:KaTeX_AMS;}.css-1d24qkw .katex .mathbb,.css-1d24qkw .katex .textbb{font-family:KaTeX_AMS;}.css-1d24qkw .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-1d24qkw .katex .mathfrak,.css-1d24qkw .katex .textfrak{font-family:KaTeX_Fraktur;}.css-1d24qkw .katex .mathtt{font-family:KaTeX_Typewriter;}.css-1d24qkw .katex .mathscr,.css-1d24qkw .katex .textscr{font-family:KaTeX_Script;}.css-1d24qkw .katex .mathsf,.css-1d24qkw .katex .textsf{font-family:KaTeX_SansSerif;}.css-1d24qkw .katex .mathboldsf,.css-1d24qkw .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-1d24qkw .katex .mathitsf,.css-1d24qkw .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-1d24qkw .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-1d24qkw .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-1d24qkw .katex .vlist-r{display:table-row;}.css-1d24qkw .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-1d24qkw .katex .vlist>span{display:block;height:0;position:relative;}.css-1d24qkw .katex .vlist>span>span{display:inline-block;}.css-1d24qkw .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-1d24qkw .katex .vlist-t2{margin-right:-2px;}.css-1d24qkw .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-1d24qkw .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-1d24qkw .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-1d24qkw .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-1d24qkw .katex .msupsub{text-align:left;}.css-1d24qkw .katex .mfrac>span>span{text-align:center;}.css-1d24qkw .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-1d24qkw .katex .mfrac .frac-line,.css-1d24qkw .katex .overline .overline-line,.css-1d24qkw .katex .underline .underline-line,.css-1d24qkw .katex .hline,.css-1d24qkw .katex .hdashline,.css-1d24qkw .katex .rule{min-height:1px;}.css-1d24qkw .katex .mspace{display:inline-block;}.css-1d24qkw .katex .llap,.css-1d24qkw .katex .rlap,.css-1d24qkw .katex .clap{width:0;position:relative;}.css-1d24qkw .katex .llap>.inner,.css-1d24qkw .katex .rlap>.inner,.css-1d24qkw .katex .clap>.inner{position:absolute;}.css-1d24qkw .katex .llap>.fix,.css-1d24qkw .katex .rlap>.fix,.css-1d24qkw .katex .clap>.fix{display:inline-block;}.css-1d24qkw .katex .llap>.inner{right:0;}.css-1d24qkw .katex .rlap>.inner,.css-1d24qkw .katex .clap>.inner{left:0;}.css-1d24qkw .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-1d24qkw .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-1d24qkw .katex .overline .overline-line,.css-1d24qkw .katex .underline .underline-line,.css-1d24qkw .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-1d24qkw .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-1d24qkw .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-1d24qkw .katex .sizing.reset-size1.size1,.css-1d24qkw .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-1d24qkw .katex .sizing.reset-size1.size2,.css-1d24qkw .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-1d24qkw .katex .sizing.reset-size1.size3,.css-1d24qkw .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-1d24qkw .katex .sizing.reset-size1.size4,.css-1d24qkw .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-1d24qkw .katex .sizing.reset-size1.size5,.css-1d24qkw .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-1d24qkw .katex .sizing.reset-size1.size6,.css-1d24qkw .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-1d24qkw .katex .sizing.reset-size1.size7,.css-1d24qkw .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-1d24qkw .katex .sizing.reset-size1.size8,.css-1d24qkw .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-1d24qkw .katex .sizing.reset-size1.size9,.css-1d24qkw .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-1d24qkw .katex .sizing.reset-size1.size10,.css-1d24qkw .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-1d24qkw .katex .sizing.reset-size1.size11,.css-1d24qkw .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-1d24qkw .katex .sizing.reset-size2.size1,.css-1d24qkw .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-1d24qkw .katex .sizing.reset-size2.size2,.css-1d24qkw .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-1d24qkw .katex .sizing.reset-size2.size3,.css-1d24qkw .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-1d24qkw .katex .sizing.reset-size2.size4,.css-1d24qkw .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-1d24qkw .katex .sizing.reset-size2.size5,.css-1d24qkw .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-1d24qkw .katex .sizing.reset-size2.size6,.css-1d24qkw .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-1d24qkw .katex .sizing.reset-size2.size7,.css-1d24qkw .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-1d24qkw .katex .sizing.reset-size2.size8,.css-1d24qkw .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-1d24qkw .katex .sizing.reset-size2.size9,.css-1d24qkw .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-1d24qkw .katex .sizing.reset-size2.size10,.css-1d24qkw .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-1d24qkw .katex .sizing.reset-size2.size11,.css-1d24qkw .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-1d24qkw .katex .sizing.reset-size3.size1,.css-1d24qkw .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-1d24qkw .katex .sizing.reset-size3.size2,.css-1d24qkw .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-1d24qkw .katex .sizing.reset-size3.size3,.css-1d24qkw .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-1d24qkw .katex .sizing.reset-size3.size4,.css-1d24qkw .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-1d24qkw .katex .sizing.reset-size3.size5,.css-1d24qkw .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-1d24qkw .katex .sizing.reset-size3.size6,.css-1d24qkw .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-1d24qkw .katex .sizing.reset-size3.size7,.css-1d24qkw .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-1d24qkw .katex .sizing.reset-size3.size8,.css-1d24qkw .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-1d24qkw .katex .sizing.reset-size3.size9,.css-1d24qkw .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-1d24qkw .katex .sizing.reset-size3.size10,.css-1d24qkw .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-1d24qkw .katex .sizing.reset-size3.size11,.css-1d24qkw .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-1d24qkw .katex .sizing.reset-size4.size1,.css-1d24qkw .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-1d24qkw .katex .sizing.reset-size4.size2,.css-1d24qkw .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-1d24qkw .katex .sizing.reset-size4.size3,.css-1d24qkw .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-1d24qkw .katex .sizing.reset-size4.size4,.css-1d24qkw .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-1d24qkw .katex .sizing.reset-size4.size5,.css-1d24qkw .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-1d24qkw .katex .sizing.reset-size4.size6,.css-1d24qkw .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-1d24qkw .katex .sizing.reset-size4.size7,.css-1d24qkw .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-1d24qkw .katex .sizing.reset-size4.size8,.css-1d24qkw .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-1d24qkw .katex .sizing.reset-size4.size9,.css-1d24qkw .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-1d24qkw .katex .sizing.reset-size4.size10,.css-1d24qkw .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-1d24qkw .katex .sizing.reset-size4.size11,.css-1d24qkw .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-1d24qkw .katex .sizing.reset-size5.size1,.css-1d24qkw .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-1d24qkw .katex .sizing.reset-size5.size2,.css-1d24qkw .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-1d24qkw .katex .sizing.reset-size5.size3,.css-1d24qkw .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-1d24qkw .katex .sizing.reset-size5.size4,.css-1d24qkw .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-1d24qkw .katex .sizing.reset-size5.size5,.css-1d24qkw .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-1d24qkw .katex .sizing.reset-size5.size6,.css-1d24qkw .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-1d24qkw .katex .sizing.reset-size5.size7,.css-1d24qkw .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-1d24qkw .katex .sizing.reset-size5.size8,.css-1d24qkw .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-1d24qkw .katex .sizing.reset-size5.size9,.css-1d24qkw .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-1d24qkw .katex .sizing.reset-size5.size10,.css-1d24qkw .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-1d24qkw .katex .sizing.reset-size5.size11,.css-1d24qkw .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-1d24qkw .katex .sizing.reset-size6.size1,.css-1d24qkw .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-1d24qkw .katex .sizing.reset-size6.size2,.css-1d24qkw .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-1d24qkw .katex .sizing.reset-size6.size3,.css-1d24qkw .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-1d24qkw .katex .sizing.reset-size6.size4,.css-1d24qkw .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-1d24qkw .katex .sizing.reset-size6.size5,.css-1d24qkw .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-1d24qkw .katex .sizing.reset-size6.size6,.css-1d24qkw .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-1d24qkw .katex .sizing.reset-size6.size7,.css-1d24qkw .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-1d24qkw .katex .sizing.reset-size6.size8,.css-1d24qkw .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-1d24qkw .katex .sizing.reset-size6.size9,.css-1d24qkw .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-1d24qkw .katex .sizing.reset-size6.size10,.css-1d24qkw .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-1d24qkw .katex .sizing.reset-size6.size11,.css-1d24qkw .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-1d24qkw .katex .sizing.reset-size7.size1,.css-1d24qkw .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-1d24qkw .katex .sizing.reset-size7.size2,.css-1d24qkw .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-1d24qkw .katex .sizing.reset-size7.size3,.css-1d24qkw .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-1d24qkw .katex .sizing.reset-size7.size4,.css-1d24qkw .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-1d24qkw .katex .sizing.reset-size7.size5,.css-1d24qkw .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-1d24qkw .katex .sizing.reset-size7.size6,.css-1d24qkw .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-1d24qkw .katex .sizing.reset-size7.size7,.css-1d24qkw .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-1d24qkw .katex .sizing.reset-size7.size8,.css-1d24qkw .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-1d24qkw .katex .sizing.reset-size7.size9,.css-1d24qkw .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-1d24qkw .katex .sizing.reset-size7.size10,.css-1d24qkw .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-1d24qkw .katex .sizing.reset-size7.size11,.css-1d24qkw .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-1d24qkw .katex .sizing.reset-size8.size1,.css-1d24qkw .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-1d24qkw .katex .sizing.reset-size8.size2,.css-1d24qkw .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-1d24qkw .katex .sizing.reset-size8.size3,.css-1d24qkw .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-1d24qkw .katex .sizing.reset-size8.size4,.css-1d24qkw .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-1d24qkw .katex .sizing.reset-size8.size5,.css-1d24qkw .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-1d24qkw .katex .sizing.reset-size8.size6,.css-1d24qkw .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-1d24qkw .katex .sizing.reset-size8.size7,.css-1d24qkw .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-1d24qkw .katex .sizing.reset-size8.size8,.css-1d24qkw .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-1d24qkw .katex .sizing.reset-size8.size9,.css-1d24qkw .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-1d24qkw .katex .sizing.reset-size8.size10,.css-1d24qkw .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-1d24qkw .katex .sizing.reset-size8.size11,.css-1d24qkw .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-1d24qkw .katex .sizing.reset-size9.size1,.css-1d24qkw .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-1d24qkw .katex .sizing.reset-size9.size2,.css-1d24qkw .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-1d24qkw .katex .sizing.reset-size9.size3,.css-1d24qkw .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-1d24qkw .katex .sizing.reset-size9.size4,.css-1d24qkw .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-1d24qkw .katex .sizing.reset-size9.size5,.css-1d24qkw .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-1d24qkw .katex .sizing.reset-size9.size6,.css-1d24qkw .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-1d24qkw .katex .sizing.reset-size9.size7,.css-1d24qkw .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-1d24qkw .katex .sizing.reset-size9.size8,.css-1d24qkw .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-1d24qkw .katex .sizing.reset-size9.size9,.css-1d24qkw .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-1d24qkw .katex .sizing.reset-size9.size10,.css-1d24qkw .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-1d24qkw .katex .sizing.reset-size9.size11,.css-1d24qkw .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-1d24qkw .katex .sizing.reset-size10.size1,.css-1d24qkw .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-1d24qkw .katex .sizing.reset-size10.size2,.css-1d24qkw .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-1d24qkw .katex .sizing.reset-size10.size3,.css-1d24qkw .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-1d24qkw .katex .sizing.reset-size10.size4,.css-1d24qkw .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-1d24qkw .katex .sizing.reset-size10.size5,.css-1d24qkw .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-1d24qkw .katex .sizing.reset-size10.size6,.css-1d24qkw .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-1d24qkw .katex .sizing.reset-size10.size7,.css-1d24qkw .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-1d24qkw .katex .sizing.reset-size10.size8,.css-1d24qkw .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-1d24qkw .katex .sizing.reset-size10.size9,.css-1d24qkw .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-1d24qkw .katex .sizing.reset-size10.size10,.css-1d24qkw .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-1d24qkw .katex .sizing.reset-size10.size11,.css-1d24qkw .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-1d24qkw .katex .sizing.reset-size11.size1,.css-1d24qkw .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-1d24qkw .katex .sizing.reset-size11.size2,.css-1d24qkw .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-1d24qkw .katex .sizing.reset-size11.size3,.css-1d24qkw .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-1d24qkw .katex .sizing.reset-size11.size4,.css-1d24qkw .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-1d24qkw .katex .sizing.reset-size11.size5,.css-1d24qkw .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-1d24qkw .katex .sizing.reset-size11.size6,.css-1d24qkw .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-1d24qkw .katex .sizing.reset-size11.size7,.css-1d24qkw .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-1d24qkw .katex .sizing.reset-size11.size8,.css-1d24qkw .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-1d24qkw .katex .sizing.reset-size11.size9,.css-1d24qkw .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-1d24qkw .katex .sizing.reset-size11.size10,.css-1d24qkw .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-1d24qkw .katex .sizing.reset-size11.size11,.css-1d24qkw .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-1d24qkw .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-1d24qkw .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-1d24qkw .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-1d24qkw .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-1d24qkw .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-1d24qkw .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-1d24qkw .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-1d24qkw .katex .delimcenter{position:relative;}.css-1d24qkw .katex .op-symbol{position:relative;}.css-1d24qkw .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-1d24qkw .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-1d24qkw .katex .op-limits>.vlist-t{text-align:center;}.css-1d24qkw .katex .accent>.vlist-t{text-align:center;}.css-1d24qkw .katex .accent .accent-body{position:relative;}.css-1d24qkw .katex .accent .accent-body:not(.accent-full){width:0;}.css-1d24qkw .katex .overlay{display:block;}.css-1d24qkw .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-1d24qkw .katex .mtable .arraycolsep{display:inline-block;}.css-1d24qkw .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-1d24qkw .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-1d24qkw .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-1d24qkw .katex .svg-align{text-align:left;}.css-1d24qkw .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-1d24qkw .katex svg path{stroke:none;}.css-1d24qkw .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-1d24qkw .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-1d24qkw .katex .stretchy::before,.css-1d24qkw .katex .stretchy::after{content:'';}.css-1d24qkw .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-1d24qkw .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-1d24qkw .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-1d24qkw .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-1d24qkw .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-1d24qkw .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-1d24qkw .katex .x-arrow-pad{padding:0 0.5em;}.css-1d24qkw .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-1d24qkw .katex .x-arrow,.css-1d24qkw .katex .mover,.css-1d24qkw .katex .munder{text-align:center;}.css-1d24qkw .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-1d24qkw .katex .fbox,.css-1d24qkw .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-1d24qkw .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-1d24qkw .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-1d24qkw .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-1d24qkw .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-1d24qkw .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-1d24qkw .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-1d24qkw .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-1d24qkw .katex .mtr-glue{width:50%;}.css-1d24qkw .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-1d24qkw .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-1d24qkw .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-1d24qkw .katex-display{display:block;margin:1em 0;text-align:center;}.css-1d24qkw .katex-display>.katex{display:block;white-space:nowrap;}.css-1d24qkw .katex-display>.katex>.katex-html{display:block;position:relative;}.css-1d24qkw .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-1d24qkw .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-1d24qkw .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-1d24qkw body{counter-reset:katexEqnNo mmlEqnNo;}.css-1d24qkw .link-like{color:#007bff;-webkit-text-decoration:underline;text-decoration:underline;}.css-1d24qkw .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-1d24qkw code,.css-1d24qkw kbd,.css-1d24qkw pre,.css-1d24qkw samp{font-family:monospace;}.css-1d24qkw code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-1d24qkw figcaption,.css-1d24qkw caption{text-align:center;}.css-1d24qkw figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-1d24qkw h3{font-size:1.75rem;}.css-1d24qkw h4{font-size:1.5rem;}.css-1d24qkw .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-1d24qkw .mathBlock .katex{font-size:24px;text-align:left;}.css-1d24qkw .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-1d24qkw .videoBlock,.css-1d24qkw .imageBlock{margin-bottom:16px;}.css-1d24qkw .imageBlock__image-align--left,.css-1d24qkw .videoBlock__video-align--left{float:left;}.css-1d24qkw .imageBlock__image-align--right,.css-1d24qkw .videoBlock__video-align--right{float:right;}.css-1d24qkw .imageBlock__image-align--center,.css-1d24qkw .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-1d24qkw .imageBlock__image-align--none,.css-1d24qkw .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-1d24qkw .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-1d24qkw .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-1d24qkw .videoBlock__caption{text-align:left;}.css-1d24qkw table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-1d24qkw .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-1d24qkw .tableBlock thead,.css-1d24qkw .tableBlock thead th{border-bottom:1px solid #333!important;}.css-1d24qkw .tableBlock th,.css-1d24qkw .tableBlock td{padding:10px;text-align:left;}.css-1d24qkw .tableBlock th{font-weight:bold!important;}.css-1d24qkw .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-1d24qkw .tableBlock caption>p{margin:0;}.css-1d24qkw .tableBlock th>p,.css-1d24qkw .tableBlock td>p{margin:0;}.css-1d24qkw .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-1d24qkw .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-1d24qkw .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-1d24qkw .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-1d24qkw .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-1d24qkw .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-1d24qkw .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-1d24qkw .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-1d24qkw .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-1d24qkw .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-1d24qkw .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-1d24qkw .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-1d24qkw .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-1d24qkw .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-1d24qkw .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-1d24qkw .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-1d24qkw .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-1d24qkw .tableBlock [data-text-align='center']{text-align:center;}.css-1d24qkw .tableBlock [data-text-align='left']{text-align:left;}.css-1d24qkw .tableBlock [data-text-align='right']{text-align:right;}.css-1d24qkw .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-1d24qkw .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-1d24qkw .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-1d24qkw .tableBlock__font-size--xxsmall{font-size:10px;}.css-1d24qkw .tableBlock__font-size--xsmall{font-size:12px;}.css-1d24qkw .tableBlock__font-size--small{font-size:14px;}.css-1d24qkw .tableBlock__font-size--large{font-size:18px;}.css-1d24qkw .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-1d24qkw .tableBlock__border--bordered td,.css-1d24qkw .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-1d24qkw .tableBlock__border--borderless tbody+tbody,.css-1d24qkw .tableBlock__border--borderless td,.css-1d24qkw .tableBlock__border--borderless th,.css-1d24qkw .tableBlock__border--borderless tr,.css-1d24qkw .tableBlock__border--borderless thead,.css-1d24qkw .tableBlock__border--borderless thead th{border:0!important;}.css-1d24qkw .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-1d24qkw .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-1d24qkw .tableBlock__table-compactl th,.css-1d24qkw .tableBlock__table-compact td{padding:3px!important;}.css-1d24qkw .tableBlock__full-size{width:100%;}.css-1d24qkw .textBlock{margin-bottom:16px;}.css-1d24qkw .textBlock__text-formatting--finePrint{font-size:12px;}.css-1d24qkw .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-1d24qkw .textBlock__text-infoBox p{margin:0;}.css-1d24qkw .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-1d24qkw .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-1d24qkw .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-1d24qkw .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-1d24qkw .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-1d24qkw .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-1d24qkw .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-1d24qkw.css-1d24qkw{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-1d24qkw.css-1d24qkw:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-1d24qkw .js-external-link-button.link-like,.css-1d24qkw .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-1d24qkw .js-external-link-button.link-like:hover,.css-1d24qkw .js-external-link-anchor:hover,.css-1d24qkw .js-external-link-button.link-like:active,.css-1d24qkw .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-1d24qkw .js-external-link-button.link-like:focus-visible,.css-1d24qkw .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-1d24qkw p,.css-1d24qkw div{margin:0;display:block;}.css-1d24qkw pre{margin:0;display:block;}.css-1d24qkw pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-1d24qkw pre:not(:first-child){padding-top:8px;}.css-1d24qkw ul,.css-1d24qkw ol{display:block margin:0;padding-left:20px;}.css-1d24qkw ul li,.css-1d24qkw ol li{padding-top:8px;}.css-1d24qkw ul ul,.css-1d24qkw ol ul,.css-1d24qkw ul ol,.css-1d24qkw ol ol{padding-top:0;}.css-1d24qkw ul:not(:first-child),.css-1d24qkw ol:not(:first-child){padding-top:4px;} Experiment specifics

Number of flips

How many times we flip the coin.

I want to have...

...this number of heads

Exactly how many heads we obtained.

Probability of heads

How likely it is to get heads (0.5 for a fair coin).

Probability of success

Probability

Chance of success

Probability of 1 in

How many times on average you'll have to repeat the flips to obtain the desired result.

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Coin flip probability – Explanation & Examples

JUMP TO TOPIC

Sample Spaces:

What is the probability of a coin landing on heads, what is the probability of a coin landing on tails, probabilities of multiple coins flip using tree diagrams, multiple flips and independent events, practice questions:, coin flip probability – explanation & examples.

Coin flip probabilities deal with events related to a single or multiple flips of a  fair coin. A fair coin has an equally likely chance of coming up Heads or Tails.

It might be advisable to refresh the following concepts to understand the material discussed in this article.

• Set theory .
• Basic Probability theory.
• Independent Events.
• Tree Diagrams .

After reading this article, you should understand:

• What is meant by coin flip probabilities.
• How to calculate probabilities associated with multiple coin flips using sample spaces.
• How to calculate probabilities associated with multiple flips using tree diagrams.
• How to calculate probabilities associated with multiple flips using the formula for probabilities of independent events.

How to calculate the probability of coin flips

To understand how to calculate the probability of coin flips, we first need to discuss the concept of sample spaces.

A sample space is a set (i.e., collection) of all possible events in a probabilistic experiment.

For example, when we flip a coin, we can either get Heads ($H$) or  Tails ($T$). So the sample space is $S=\{H, T\}$. Every subset of a sample space is called an event . For a single toss of a coin, we can make four subsets of the sample space, i.e., the empty set $\Phi$, $\{H\}$, $\{T\}$ and the sample space itself $\{H, T\}$. The probability of an empty set (i.e., neither Heads nor Tails) is always zero, and the probability of the entire sample space ( i.e., either Heads or Tails) is always $1$. For any other given event $E$ (i.e., a subset of $S$), we can use the following formula

$\fbox{$P(E) = \frac{\textrm{Number of elements in E}}{\textrm{Number of elements in S}}$}$     

To calculate the probability of the event $E=\{H\}$, we note that $E$ contains only one element and sample space $S$ contains two elements, so

$P(\{H\}) = \frac{1}{2}$.

Using a similar argument, the probability of the event $E=\{T\}$ is given as

$P(\{T\}) = \frac{1}{2}$.

How to calculate the probability of multiple coin flips

Only a small number of questions can be asked about the probabilities associated with a single flip of a coin. However, we can ask many interesting questions if we consider multiple flips of a coin (Note: we get the same sample space whether we flip a single coin multiple times or flip multiple coins simultaneously).

Let us consider the experiment of flipping a fair coin twice: we can write the corresponding sample space as $S = \{HH, HT, TH, TT\}$. Let us find the probabilities associated with this experiment.

Example 1 : A  fair coin is flipped twice. What is the probability of the following events:

• Getting at least one Heads.
• Getting at most one Heads.
• Getting Tails twice. 
• Getting no Tails.

1) Getting at least one Heads

Let $E$ be the event that we get at least one head. We can see from the sample space that there are three possibilities of getting at least one Head, i.e., the first flip is Heads and second Tails, the first flip is Tails and the second head, and both flips are Heads. Hence, $E = \{HT, TH, HH\}$. Note that there are three elements in $E$ and a total of 4 elements in $S$; therefore,

$P(\textrm{Atleast one Heads}) = P(E) = \frac34$.

2) Getting at most one Heads

Let $E$ be the event that we get at most one head. Then, $E=\{HT, TH, TT\}$. We note that $E$ has three elements and sample space $S$ has 4 elements, so

$P(\textrm{At most one Heads}) = P(E) = \frac34$.

3) Getting Tails twice

Let $E$ be the event that we get tails twice. Then, $E=\{TT\}$. We note that $E$ has one element and sample space $S$ has 4 elements, so

$P(\textrm{two tails}) = P(E) = \frac14$.

4) Getting no Tails

Let $E$ be the event that we get no tails. Then, $E=\{HH\}$. We note that $E$ has one element and sample space $S$ has 4 elements, so

$P(\textrm{no tails}) = P(E) = \frac14$.

Example 2 : A fair coin is flipped three times. Make the sample space and find the probabilities of the following events:

• Getting all Heads.
• Getting all Tails.
• Getting an even number of Tails.
• Getting more Heads than Tails.

We can write the sample space as $S=\{HHH,HHT,HTH,HTT,THH,THT,TTH,TTT\}$.

1) Getting all Heads

Let $E$ be the event that we get all heads. We can see from the sample space that there is only one outcome with three heads, i.e., $E = \{HHH\}$. So the probability is

$P(E) = \frac{\textrm{Number of elements in E}}{\textrm{Number of elements in S}}=\frac18$.

2) Getting all tails

Let $E$ be the event that we get all tails. We can see from the sample space that there is only one outcome with all tails, i.e.,$E = \{TTT\}$. So the probability is

3) Getting an even number of tails

Let $E$ be the event that we get an even number of tails. We can see from the sample space that there are three outcomes with an even number of tails, i.e., $E = \{HTT, THT, TTH\}$. So the probability is

$P(E) = \frac{\textrm{Number of elements in E}}{\textrm{Number of elements in S}}=\frac38$

4) Getting more heads than tails

Let $E$ be the event that we get more heads than tails. We can see from the sample space that four outcomes have more heads than tails, i.e., $E = \{HHH, HHT, HTH, THH\}$. So the probability is

$P(E) = \frac{\textrm{Number of elements in E}}{\textrm{Number of elements in S}}=\frac48=\frac12$.

It is more convenient to rely on tree-diagrams to find multiple coin flip probabilities than to use the sample space method in many cases. We illustrate the concept using examples

Example 3 :

A coin is flipped three times. Draw a tree diagram that represents all possible outcomes. Also, calculate the probabilities of the following events: 

• Getting three Heads.
•  Getting two Tails.
•  Getting no Heads.
•  Getting at least one Tails.

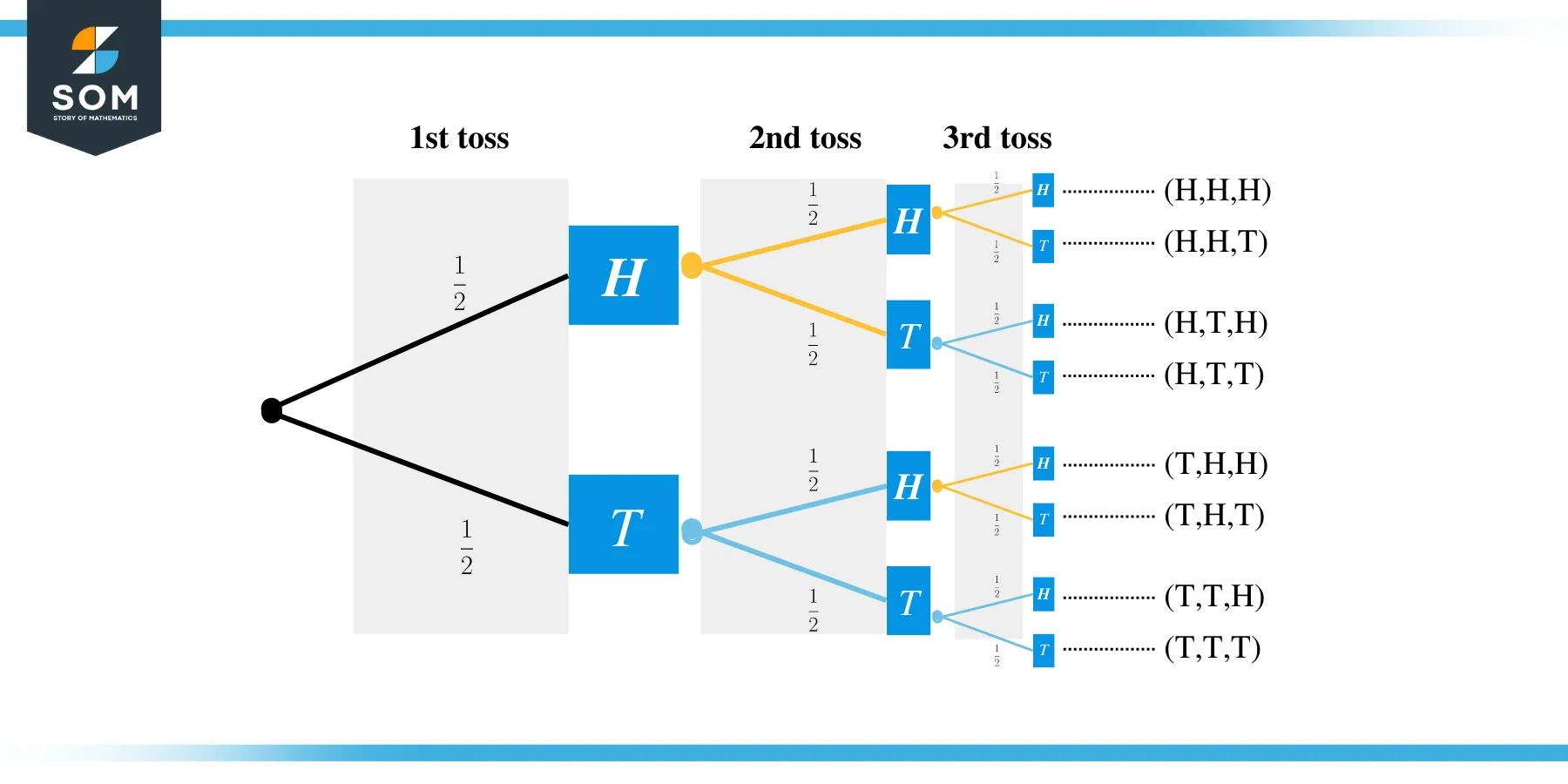
1) Getting three Heads

From the tree diagram, we can see that only one outcome corresponds to the event of getting all three heads. To get probabilities out of a tree diagram, we multiply the probabilities along the branches. So, the probability of getting three heads is

$P(\textrm{Three Heads}) =  \frac12 \times \frac12 \times \frac12=\frac18$.

2) Getting two Tails

We can see that there are three events that have two tails,i.e., $E1=\{TTH\}$, $E2=\{HTT\}$ and $E3=\{THT\}$. So we will add the probabilities of each event:

$P(E1)=\frac12 \times \frac12 \times \frac12=\frac18$.

$P(E2)=\frac12 \times \frac12 \times \frac12=\frac18$.

$P(E3)=\frac12 \times \frac12 \times \frac12=\frac18$.

So we can write the probability of getting two tails as

$P(\textrm{Two Tails}) = P(E1)+P(E2)+P(E3) = \frac18+\frac18+\frac18=\frac{3}{8}$.

3) Getting no Heads

From the tree diagram, we can see that the probability of getting no Heads is

$P(\textrm{no Heads}) =  \frac12 \times \frac12 \times \frac12=\frac18$.

4) Getting at least one Tails

We can see that there are six events that have at least one tails, i.e., $E1=\{TTH\}$, $E2=\{HTT\}$, $E3=\{THH\}$, $E4=\{THT\}$, $E5=\{TTH\}$, and $E6=\{TTT\}$. So we will add the probabilites of each event:

$P(E4)=\frac12 \times \frac12 \times \frac12=\frac18$.

$P(E5)=\frac12 \times \frac12 \times \frac12=\frac18$.

$P(E6)=\frac12 \times \frac12 \times \frac12=\frac18$.

So we can write the probability of getting at least one tails as

$P(\textrm{Two Tails}) = P(E1)+P(E2)+P(E3)+P(E4)+P(E5)+P(E6) $

                          $= \frac18+\frac18+\frac18+\frac18+\frac18+\frac18=\frac{6}{8}=\frac{3}{4}$.

When the number of flips is large, both the tree diagrams and the sample space methods might become too cumbersome. In such cases, we can rely on the fact that multiple flips are independent events.  Two events are said to be independent if one event does not affect the probabilities of the other . When we flip a coin multiple times, the outcome of any one flip does not affect the other flips’ outcomes, so the events are independent. Remember from basic probability theory that when two events, say $E1$ and $E2$, are independent, the probability of the event $E1$ AND $E2$ is given as

$P(E1\; \textrm{AND}\; E2) = P(E1) \times P(E2)$

We can use the above expression to solve multiple coin flips’ problems, as shown in the examples below.

Example 4: A fair coin is flipped twice. What is the probability of the following events:

We have already solved this example using the sample space method. Now, we solve it using the concept of independent probabilities.

We first find the probability of finding no Heads, i.e., the probability that both flips are Tails.

$P(\textrm{First flip is Tails}) = \frac12$.

$P(\textrm{Second flip is Tails}) = \frac12$.

$P(\textrm{First flip is Tails AND Second flip is Tails}) = \frac12 \times \frac12 = \frac14$.

Since both flips are independent, so we have multiplied the probabilities. Now, from basic probability theory, we know that

$P(\textrm{Atleast one Heads}) = 1  – P(\textrm{Getting no Heads}) = 1 – \frac14 = \frac34$.

Three possibilities correspond to getting at most one Heads, i.e., $\{TT\}$, $\{HT\}$, and $\{TH\}$.  Using the concept of independent events, we evaluate each possibility’s probability and then add to get the final answer.

$P(\{TT\}) = \frac12 \times \frac12 = \frac14$.

$P(\{HT\}) = \frac12 \times \frac12 = \frac14$.

$P\{TH\} = \frac12 \times \frac12 = \frac14$.

$P(\textrm{At most one Heads}) = P(\{TT\}) + P(\{HT\}) + P(\{TH\}) = \frac14 + \frac14 + \frac14 = \frac34$.

  3) Getting Tails twice

Getting Tails twice is the same as the first flip is Tails, AND the second flip is Tails. Therefore,

$P(\textrm{getting Tails twice}) = P((\textrm{first flip is Tails}) \times P(\textrm{Second flip is Tails) = \frac12 \times \frac12 = \frac14$.

$P(\textrm{Getting no Tails})  = P(\textrm{First flip is not Tails}) \times P(\textrm{Second flip is not Tails})$.

$P(\textrm{First flip is not Tails}) = 1 – P(\textrm{First flip is Tails}) =1 -\frac12 = \frac12$.

$P(\textrm{Second flip is not Tails}) = \frac12$. Hence,

$P(\textrm{Getting no Tails}) = \frac12 \times \frac12 = \frac14$.

Example 5: A coin is flipped $10$ times. What are the probabilities of getting:

• At least one Heads.

Note that we are flipping the coin $10$ times. Both the sample space and the tree diagram will make the question too complex. However, using the concept of independent events, we can easily solve this question.

$P(\textrm{getting at least one Heads}) = 1 – p(\textrm{getting no Heads)\}$.

Now, getting no Heads is the same as getting Tails $10$ times in $10$ flips. In each flip, the probability of getting a Tails is $\frac12$. Since each flip is independent, so the probability will get multiplied, i.e.,

$P(\textrm{10 tails in 10 flips}) = \left(\frac12\right)^{10}$. Finally,

$P(\textrm{getting at least one Heads}) = 1 – \left(\frac12\right)^{10} = 0.999$.

Example 6: A coin is flipped multiple times. What is the probability that the first Heads come up on the 4th flip?

$P(\textrm{first Heads on 4th flip}) = P(\textrm{1st Tails AND 2nd Tails AND 3rd Tails AND 4th Heads})$.

$P(\textrm{first Heads on 4th flip}) = P(\textrm{1st Tails}) \times P(\textrm{2nd Tails})  \times P(\textrm{3rd Tails}) \times P(\textrm{4th Heads}) $.

$P(\textrm{first Heads on 4th flip}) = \frac12 \times \frac12 \times \frac12 \times \frac12 = \frac{1}{16}$.

• A coin is flipped 4 times. Draw a tree diagram to show the probability that three heads and one tail appear?

Three fair coins are tossed simultaneously. What is the probability of the following:

• The first is the head, and the second is the tail.
• Three heads in a row.
• Two tails and one head.

Three fair coins are tossed simultaneously. Use a tree diagram to determine the probability of getting:

• At least 2 Tails.
• At most two Heads.
• No Tails at all.
• The coin comes up Heads for the first time after 3 attempts.
• First Heads in the first three attempts.

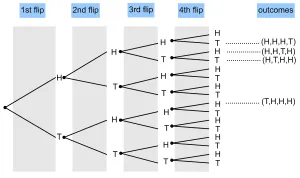
$P(\textrm{3 Heads and 1 Tails}) = \frac{4}{16} = \frac14$.

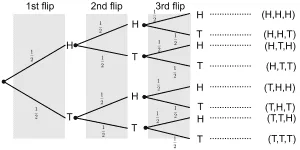
$P(\textrm{atleast two Tails}) = P(T,T,H) + P(T,H,T) + P(H,T,T) + P(T,T,T) = \frac12$.

$P(\textrm{at most two Heads}) = 1 – P(H,H,H) = \frac78$.

$P(\textrm{No tails}) = P(H,H,H) = \frac18$.

Previous Lesson  |  Main Page | Next Lesson

Flip a coin

In the study of probability, flipping a coin is a commonly used example of a simple experiment. When a fair, two-sided coin is flipped, the two possible outcomes are heads (left) or tails (right), as shown in the figure below.

The sample space of an experiment is the set of all possible outcomes of an experiment. The sample space for flipping a coin can be denoted as

where H is heads and T is tails.

Each of the two possible outcomes has an equal likelihood of occurring, assuming that the coin is fair. Given that A represents the event that heads occurs, and B represents the event where tails occurs, the probability, P, of heads occurring can be denoted as P(A) = 1/2. Similarly, the probability of tails occurring can be denoted as P(B) = 1/2.

For any flip of a fair, two-sided coin, only heads or tails can occur. Thus, the outcomes of the flip of a coin are said to be mutually exclusive events since both events cannot occur at the same time. Also, because any one flip of the coin has no bearing on the outcome of another flip, each flip of a coin is an independent-event .

Sample space when more than one coin is flipped

When two or more coins are flipped the sample space can be denoted as:

{HH, HT, TH, TT}

Note that although the outcomes TH and HT both have one heads and one tails, they are considered different outcomes. The probability that any one of these events occurs is 1/4.

Similarly, the sample space for flipping three coins can be denoted as:

{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

The probability that any one of these events occurs is 1/8.

Notice that when one coin is flipped, the sample space contains 2 possible outcomes; when two coins are flipped, the sample space contains 4, or 2 2 outcomes; when three coins are flipped, the sample space contains 8, or 2 3 outcomes, and so on. The number of outcomes is therefore a function of the number of coins flipped, and is equal to 2 n . Knowing the sample space allows us to compute various probabilities.

Probabilities with two or more coin flips

Given the sample space of an experiment, the probability of any event occurring can be calculated by dividing the number of outcomes that fulfill the desired criteria by the total number of possible outcomes.

For example, the sample space for flipping two fair two-sided coins is:

If we wanted to determine the probability that a coin that is flipped twice first lands on heads, and then lands on tails, there is only one way that this outcome can occur, since order matters. Thus, out of 4 possible outcomes, only 1 yields the desired result, and the probability of this outcome (A) is:

If we instead wanted to determine the probability that, of the two flips, only one results in a coin landing on heads, there are two possible ways that this can occur: HT or TH. Thus, the probability of this outcome (A) is:

P(A) = 2/4 = 1/2

Similarly, if a coin were flipped three times, the sample space is:

If the desired outcome (A) is at least two heads occurring, there are three possible ways that this can occur: HHT, HTH, THH. The probability of this outcome is therefore:

These probabilities are relatively simple to calculate, since the sample space does not contain many possible outcomes, and the experiment is simple. However, the concept can be extended to more complicated examples, and formulas exist for computing these types of probabilities. For example, the probability of two or more independent events occurring is the product of their probabilities. In the case of flipping a coin, the probability of heads or tails occurring is always 1/2, so for an experiment in which a coin is flipped n times, the probability of observing any one of the possible outcomes (A) in the sample space can be computed as:

P(A) = (1/2) n

where n is the number of times a fair, two-sided coin is flipped.

When a coin is flipped twice,

P(A) = (1/2) 2 = 1/4

Similarly, when a coin is flipped three times:

P(A) = (1/2) 3 = 1/8