Word problems on Pythagorean Theorem
Learn how to solve different types of word problems on Pythagorean Theorem .
Pythagoras Theorem can be used to solve the problems step-by-step when we know the length of two sides of a right angled triangle and we need to get the length of the third side.
Three cases of word problems on Pythagorean Theorem :
Case 1: To find the hypotenuse where perpendicular and base are given.
Case 2: To find the base where perpendicular and hypotenuse are given.
Case 3: To find the perpendicular where base and hypotenuse are given.
Word problems using the Pythagorean Theorem:
1. A person has to walk 100 m to go from position X in the north of east direction to the position B and then to the west of Y to reach finally at position Z. The position Z is situated at the north of X and at a distance of 60 m from X. Find the distance between X and Y.
|
Let XY = x m Therefore, YZ = (100 – x) m
In ∆ XYZ, ∠Z = 90° Therefore, by Pythagoras theorem XY = YZ + XZ⇒ x = (100 – x) + 60 ⇒ = 10000 – 200x + + 3600 |
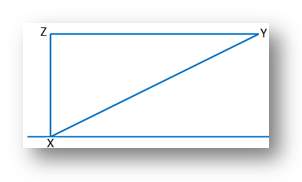
⇒ 200x = 10000 + 3600
⇒ 200x = 13600
⇒ x = 13600/200
Therefore, distance between X and Y = 68 meters.
Therefore, length of each side is 8 cm.
Using the formula solve more word problems on Pythagorean Theorem.
3. Find the perimeter of a rectangle whose length is 150 m and the diagonal is 170 m.
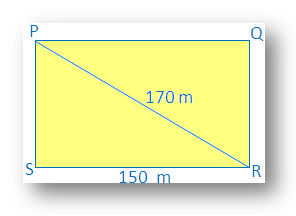
In a rectangle, each angle measures 90°.
Therefore PSR is right angled at S
Using Pythagoras theorem, we get
⇒ PS = √6400
Therefore perimeter of the rectangle PQRS = 2 (length + width)
= 2 (150 + 80) m
= 2 (230) m
= 460 m
4. A ladder 13 m long is placed on the ground in such a way that it touches the top of a vertical wall 12 m high. Find the distance of the foot of the ladder from the bottom of the wall.
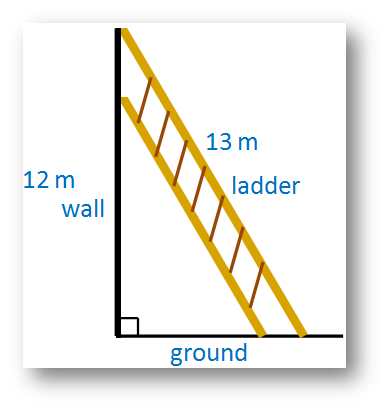
Let the required distance be x meters. Here, the ladder, the wall and the ground from a right-angled triangle. The ladder is the hypotenuse of that triangle.
According to Pythagorean Theorem,
Therefore, distance of the foot of the ladder from the bottom of the wall = 5 meters.
5. The height of two building is 34 m and 29 m respectively. If the distance between the two building is 12 m, find the distance between their tops.
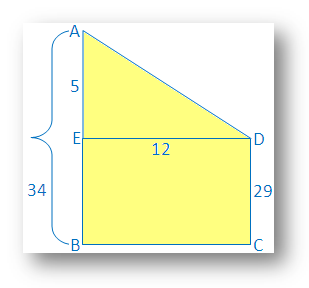
The vertical buildings AB and CD are 34 m and 29 m respectively.
Draw DE ┴ AB
Then AE = AB – EB but EB = BC
Therefore AE = 34 m - 29 m = 5 m
Now, AED is right angled triangle and right angled at E.
⇒ AD = √169
Therefore the distance between their tops = 13 m.
The examples will help us to solve various types of word problems on Pythagorean Theorem.
Congruent Shapes
Congruent Line-segments
Congruent Angles
Congruent Triangles
Conditions for the Congruence of Triangles
Side Side Side Congruence
Side Angle Side Congruence
Angle Side Angle Congruence
Angle Angle Side Congruence
Right Angle Hypotenuse Side congruence
Pythagorean Theorem
Proof of Pythagorean Theorem
Converse of Pythagorean Theorem
7th Grade Math Problems 8th Grade Math Practice From Word problems on Pythagorean Theorem to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
Share this page: What’s this?
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
Adding 2-digit numbers | add two two-digit numbers without carrying.
Sep 19, 24 03:22 PM
Adding 1-Digit Number | Understand the Concept one Digit Number
Sep 19, 24 03:18 PM
Addition Word Problems - 1-Digit Numbers | Basic Concept on Addition
Sep 19, 24 01:29 AM
Addition of Three 1-Digit Numbers | Add 3 Single Digit Numbers | Steps
Sep 19, 24 01:15 AM
Addition of Numbers using Number Line | Addition Rules on Number Line
Sep 18, 24 02:47 PM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Free ready-to-use math resources
Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth
15 Pythagorean Theorem Practice Problems For 8th Grade
Beki Christian
Pythagorean Theorem practice problems involve using the relationship between the sides of a right triangle to calculate missing side lengths in triangles. The Pythagorean Theorem is introduced in 8th grade and is used to solve a variety of problems across high school.
Here, you’ll find a selection of Pythagorean Theorem questions that demonstrate the different types of questions students are likely to encounter in 8th grade.
What is the Pythagorean Theorem?
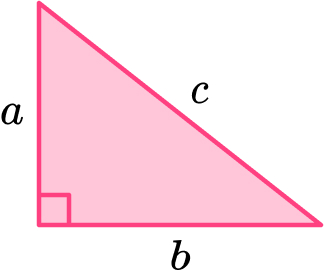
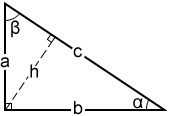
The Pythagorean Theorem is the geometric theorem that states that the square of the hypotenuse (longest side) of a right triangle is equal to the sum of the squares of the two shorter sides of the triangle.
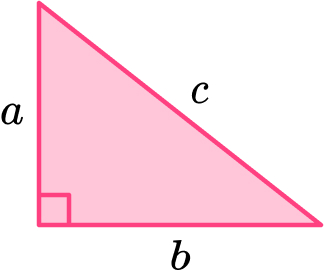
This can be written as a^2+b^2=c^2 for a triangle labeled like this:
15 Pythagoras Theorem Practice Problems
Find all of the Pythagoras Theorem questions included in this blog in this easy to download resource. Suitable for 8th grade students. Includes answer key.
How to answer Pythagorean Theorem questions
1 – Label the sides of the triangle a , b , and c . Note that the hypotenuse, the longest side of a right triangle, is opposite the right angle and will always be labeled .
2 – Write down the formula and substitute the values>
3 – Calculate the answer. You may be asked to give your answer in an exact form or round to a given degree of accuracy, such as a certain number of decimal places or significant figures.
Pythagorean Theorem in real life
Pythagorean Theorem has many real-life uses, including in architecture and construction, navigation and surveying.
Pythagorean Theorem in 8th grade
Pythagorean Theorem is usually introduced in middle school, as it is a part of the 8th grade Common Core Math Standards.
The emphasis in middle school is on students being able to:
- Explain the Pythagorean Theorem;
- Use the theorem to solve mathematical and real-world problems – with both 2D and 3D figures;
- Use the theorem to calculate the distance between two points on a coordinate grid.
The process for solving any Pythagoras Theorem problem always begins by identifying the relevant right-angled triangle and labeling the sides a , b , c. If there is not a diagram in the question, it can be helpful to draw one.
Where necessary, round your answers to 3 significant figures.
Pythagorean Theorem practice problems
1. A ship sails 6 \, km East and then 8 \, km North. Find the ship’s distance from its starting point.
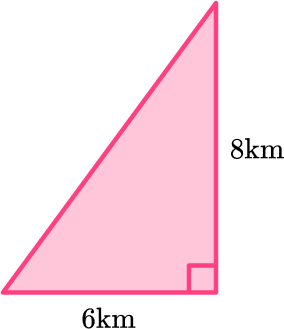
The ship is 10 kilometers from its starting point.
2. A ladder is 5 \, m long. The base of the ladder is 3 \, m from the base of a vertical wall. How far up the wall does the ladder reach?
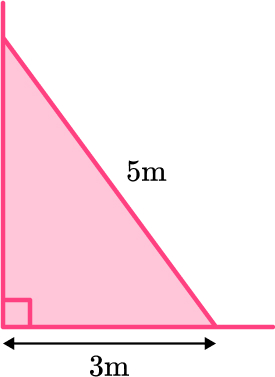
The ladder reaches 4 meters up the wall.
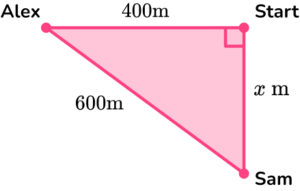
3. Alex and Sam start from the same point. Alex walks 400 meters west. Sam walks x meters south, until they are 600 \, m apart from each other. How far does Sam walk?
4. A television’s size is the measurement from the upper left hand corner of the television to the bottom right hand corner. Find the size of this television.
39.7 inches
55.1 inches
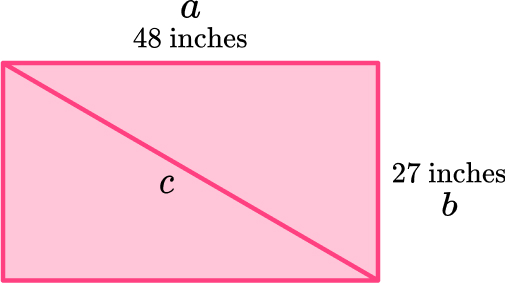
5. The pole of a sailing boat is supported by a rope from the top of the pole to an anchor point on the deck. The pole is 4 \, m long and the rope is 4.5 \, m long. Calculate the distance from the base of the pole to the anchor point of the rope on the deck.
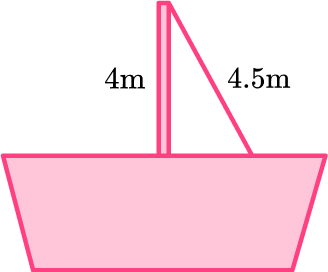
6. Work out the length of the diagonal of a square with 8 \, cm sides.
The diagonal of the square has a length of 11.3 centimeters.
7. ABC is an isosceles triangle.
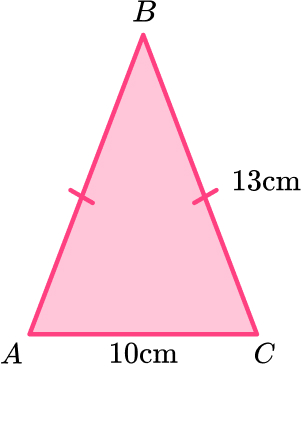
Work out the height of the triangle.
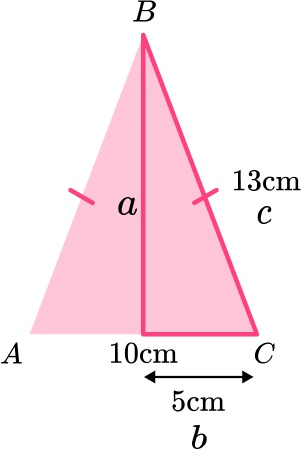
8. ABCD is an isosceles trapezoid.
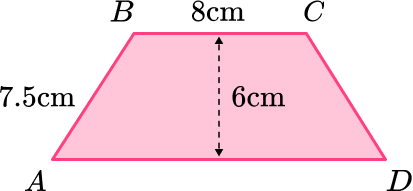
Work out the length of AD.
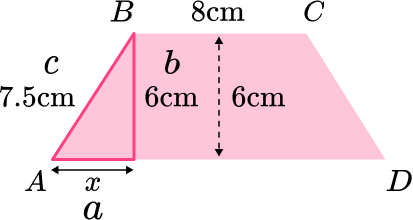
9. Here is a cm square grid. Calculate the distance between the points A and B.
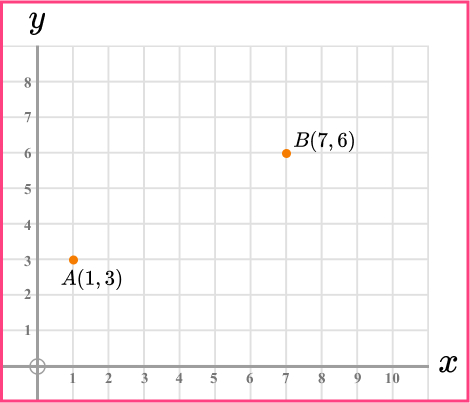
10. Which is a right angled triangle?
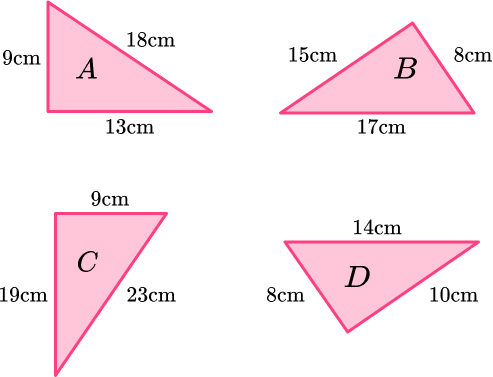
Not a right angled triangle because Pythagorean Theorem doesn’t work.
Right angled triangle because Pythagorean Theorem works.
11. PQRS is made from two right angled triangles.
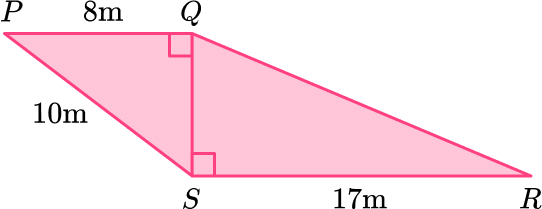
Work out the length of QR.
Triangle \text{PQS:}
Triangle \text{QRS}
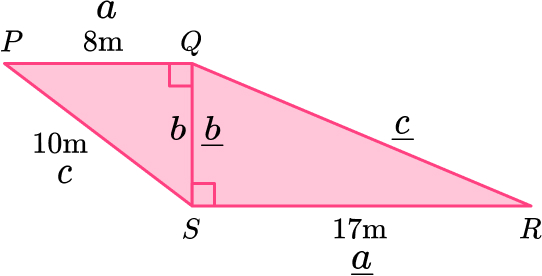
12. Here is a pattern made from right angled triangles. Work out the length x.
Triangle \text{ABC:}
Triangle \text{ACD:}
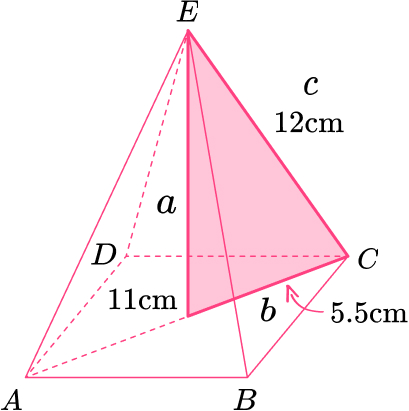
13. Here is a pyramid.
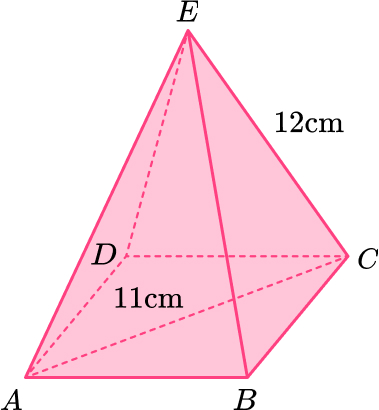
Work out the height of the pyramid.
14. Here is a cuboid.
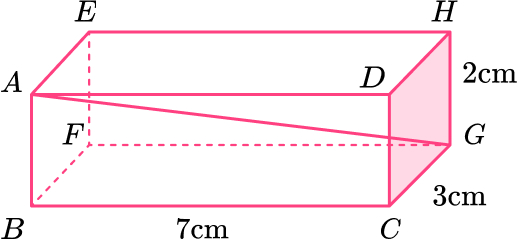
Work out the length AG.
Give your answer in its exact form.
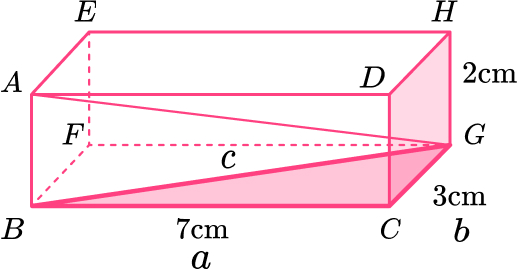
Length of \text{BG:}
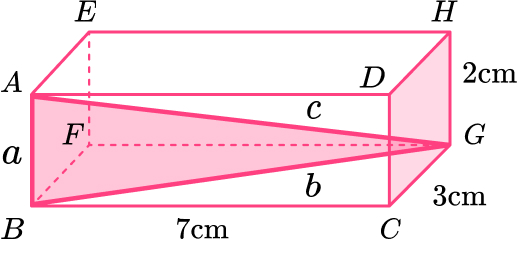
Length of \text{AG:}
15. Here is a right angled triangle.
Form an equation and use it to work out the value of x.
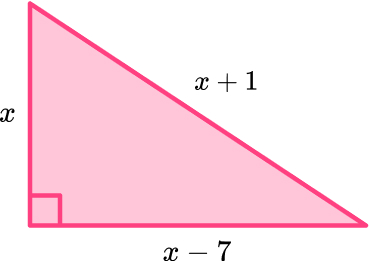
x=4 \, or \, x=12
x cannot be 4 as you can’t have a negative side length so x=12
Pythagorean Theorem in middle school
In middle school, students…
- prove the Pythagorean Theorem;
- use the Pythagorean Theorem with trigonometric ratios to solve problems;
- use the Pythagorean Theorem in proofs.
Pythagoras Theorem may feature in questions alongside other topics, such as trigonometry, circle theorems or algebra.
The Pythagorean Theorem is used to calculate a missing length in a right triangle . If you have a right angled triangle and you know two of the lengths, label the sides of the triangle a,b and c (c must be the hypotenuse – the longest side). Pythagorean Theorem is a^2+b^2=c^2. Substitute the values you know into Pythagorean Theorem and solve to find the missing side.
The hypotenuse of a right triangle is the longest side. If you know the lengths of the other two sides, you can find the length of the hypotenuse by squaring the two shorter sides, adding those values together and then taking the square root. By doing this you are finding c in a^2+b^2=c^2
If your triangle is a right triangle and you know two of the sides, you can use Pythagorean Theorem to find the length of the third side. To do this, label the sides a , b and c (with c being the hypotenuse – the longest side). Substitute the values you know into a^2+b^2=c^2 and solve to find the missing side.
Looking for more Pythagorean theorem math questions?
- Ratio questions
- Algebra questions
- Probability questions
- Trigonometry questions
- Venn diagram questions
- Long division questions
RELATED RESOURCE :
- 6th Grade Math Problems
- 7th Grade Math Problems
- 8th grade math problems
Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?
The content in this article was originally written by former UK Secondary teacher Beki Christian and has since been revised and adapted for US schools by elementary and middle school teacher Kathleen Epperson.
Related articles
34 6th Grade Math Problems: Answers With Worked Examples
24 Ratio Word Problems for Grades 6-7 With Tips On Supporting Students’ Progress
7 Questions You Should Ask When Reviewing Your Current Or Future Math Curriculum
The 12 Divisibility Rules You Need To Know (With A New One You’ve Probably Never Heard Of)
Math Games for 6th Graders [FREE]
On the lookout to make your math lessons fun and interactive while building math skills? Try our 6 printable math games for 6th graders.
Playable in pairs, teams or a whole class, our accompanying instructions and printable resources make preparation a breeze!
Privacy Overview
- Science Notes Posts
- Contact Science Notes
- Todd Helmenstine Biography
- Anne Helmenstine Biography
- Free Printable Periodic Tables (PDF and PNG)
- Periodic Table Wallpapers
- Interactive Periodic Table
- Periodic Table Posters
- Science Experiments for Kids
- How to Grow Crystals
- Chemistry Projects
- Fire and Flames Projects
- Holiday Science
- Chemistry Problems With Answers
- Physics Problems
- Unit Conversion Example Problems
- Chemistry Worksheets
- Biology Worksheets
- Periodic Table Worksheets
- Physical Science Worksheets
- Science Lab Worksheets
- My Amazon Books
Pythagorean Theorem – Definition, Formula, Problems
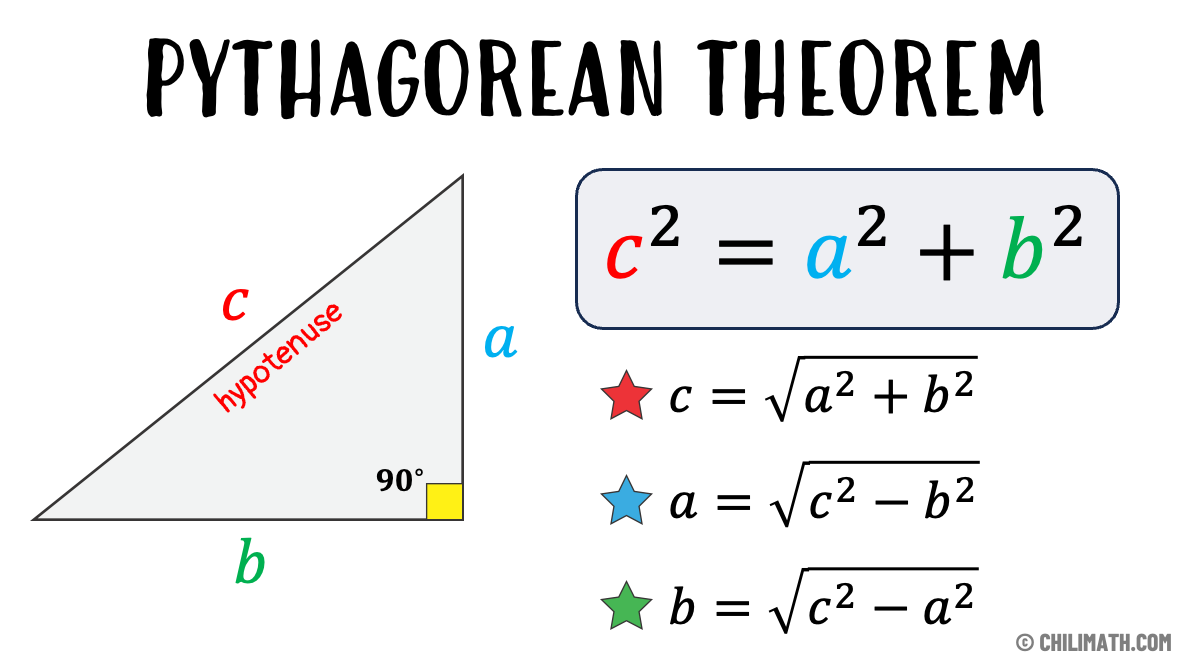
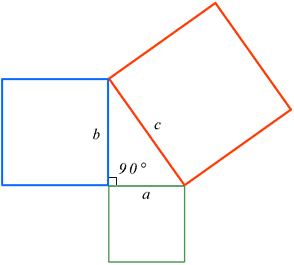
In mathematic, the Pythagorean theorem states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of its other two sides . Another way of stating the theorem is that the sum of the areas of the squares formed by the sides of a right triangle equals the area of the square whose side is the hypotenuse. The theorem is a key relation in Euclidean geometry. It is named for the Greek philosopher Pythagorus.
Remember: The Pythagorean theorem only applies to right triangles!
Pythagorean Theorem Formula
The formula for the Pythagorean theorem describes the relationship between the sides a and b of a right triangle to its hypotenuse, c . A right triangle is one containing a 90° or right angle. The hypotenuse is the side of the triangle opposite from the right angle (which is the largest angle in a right triangle).
a 2 + b 2 = c 2
Solving for a, b, and c
Rearranging the equation gives the formulas solving for a, b, and c:
- a = (c 2 – b 2 ) ½
- b = (c 2 – a 2 ) ½
- c = (a 2 + b 2 ) ½
How to Solve the Pythagorean Theorem – Example Problems
For example, find the hypotenuse of a right triangle with side that have lengths of 5 and 12.
Start with the formula for the Pythagorean theorem and plug in the numbers for the sides a and b to solve for c .
a 2 + b 2 = c 2 5 2 + 12 2 = c 2 c 2 = 5 2 + 12 2 = 25 + 144 = 169 c2 = 169 c = √169 or 169 ½ = 13
For example, solve for side b of a triangle where a is 9 and the hypotenuse c is 15.
a 2 + b 2 = c 2 9 2 + b 2 = 15 2 b 2 = 15 2 – 9 2 = 225 – 81 = 144 b = √144 = 12
Now, let’s combine a bit of algebra with the geometry. Solve for x where the sides of a right triangle are 5x and 4x +5 and the hypotenuse has a length of 8x -3.
a 2 + b 2 = c 2 (5x) 2 + (4x +5) 2 = (8x-3) 2
The (4x + 5) 2 and (8x -3)2 terms are the squares of binomial expressions. So, expanding the equation gives the following:
25x 2 + (4x +5)(4x +5) = (8x -3)(8x -3) 25x 2 = 16×2 + 20x +20x + 25 = 64x – 24x – 24x + 9
Combine like terms:
41x 2 + 40x + 25 = 64x 2 – 48x + 9
Rewrite the equation and solve for x.
0 = 23x 2 – 88x – 16
Apply the quadratic equation and solve for x:
x = [-b ± √(b 2 -4ac)]/2a x = [-(-88) ± √[-88 2 – 4(23)(-16)] / 2(23) = [88 ± √(7744 + 1472)] / 46 = (88 ± 96) / 46
So, there are two answers:
x = (88 + 96)/46 = 4 and (88 – 96).46 = -4/23
A triangle does not have a negative length for its side, so x is 4.
Plugging in”4″ in place of x, the sides of the right triangle are 20, 21, and 29.
Pythagorean Triples
Pythagorean triples are integers a, b, and c, that represent the sides of a right triangle and satisfy the Pythagorean theorem. Here is the list of Pythagorean triples for integers with values less than 100:
(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Proof of the Pythagorean Theorem
There are more proofs for the Pythagorean theorem than for any other theorem in geometry! At least 370 proofs are known. Some of these proofs use the parallel postulate. Some rely on the complementarity of acute angles in a right triangle. Proofs using shearing use the properties of parallelograms.
History – Did Pythagoras Discover the Pythagorean Theorem?
While the Pythagorean theorem takes its name from Pythagorus, he did not discover it. Exactly who gets the credit or whether many different places made the discovery independently is a matter of debate. The Mesopotamians made calculations using the formula as early as 2000 BC, which was over a thousand years before Pythagorus. A papyrus from the Egyptian Middle Kingdom, dating between 2000 and 1786 BC, references a math problem describing Pythagorean triples. The Baudhayana Shulba Sutra from India (dating between the 8th and 5th century BC) lists both Pythagorean triples and the Pythagorean theorem. The “Gougu theorem” from China offers a proof for the Pythagorean theorem, which came into use long before its oldest surviving description from the 1st century BC.
Pythagorus of Samos lived between 570 and 495 BC. While he was not the original person who formulated the Pythagorean theorem, he (or his students) may have introduced its proof to ancient Greece. In any case, his philosophical treatment of math left a lasting impression on the world.
- Bell, John L. (1999). The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development . Kluwer. ISBN 0-7923-5972-0.
- Heath, Sir Thomas (1921). “ The ‘Theorem of Pythagoras ‘”. A History of Greek Mathematics (2 Vols.) (Dover Publications, Inc. (1981) ed.). Oxford: Clarendon Press. ISBN 0-486-24073-8.
- Maor, Eli (2007). The Pythagorean Theorem: A 4,000-Year History . Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
- Swetz, Frank; Kao, T. I. (1977). Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China . Pennsylvania State University Press. ISBN 0-271-01238-2.
Related Posts
- Home |
- About |
- Contact Us |
- Privacy |
- Newsletter |
- Shop |
- 🔍 Search Site
- Easter Color By Number Sheets
- Printable Easter Dot to Dot
- Easter Worksheets for kids
- Kindergarten
- All Generated Sheets
- Place Value Generated Sheets
- Addition Generated Sheets
- Subtraction Generated Sheets
- Multiplication Generated Sheets
- Division Generated Sheets
- Money Generated Sheets
- Negative Numbers Generated Sheets
- Fraction Generated Sheets
- Place Value Zones
- Number Bonds
- Addition & Subtraction
- Times Tables
- Fraction & Percent Zones
- All Calculators
- Fraction Calculators
- Percent calculators
- Area & Volume Calculators
- Age Calculator
- Height Calculator
- Roman Numeral Calculator
- Coloring Pages
- Fun Math Sheets
- Math Puzzles
- Mental Math Sheets
- Online Times Tables
- Online Addition & Subtraction
- Math Grab Packs
- All Math Quizzes
- Kindergarten Math Quizzes
- 1st Grade Quizzes
- 2nd Grade Quizzes
- 3rd Grade Quizzes
- 4th Grade Quizzes
- 5th Grade Quizzes
- 6th Grade Math Quizzes
- Place Value
- Rounding Numbers
- Comparing Numbers
- Number Lines
- Prime Numbers
- Negative Numbers
- Roman Numerals
- Subtraction
- Add & Subtract
- Multiplication
- Fraction Worksheets
- Learning Fractions
- Fraction Printables
- Percent Worksheets & Help
- All Geometry
- 2d Shapes Worksheets
- 3d Shapes Worksheets
- Shape Properties
- Geometry Cheat Sheets
- Printable Shapes
- Coordinates
- Measurement
- Math Conversion
- Statistics Worksheets
- Bar Graph Worksheets
- Venn Diagrams
- All Word Problems
- Finding all possibilities
- Logic Problems
- Ratio Word Problems
- All UK Maths Sheets
- Year 1 Maths Worksheets
- Year 2 Maths Worksheets
- Year 3 Maths Worksheets
- Year 4 Maths Worksheets
- Year 5 Maths Worksheets
- Year 6 Maths Worksheets
- All AU Maths Sheets
- Kindergarten Maths Australia
- Year 1 Maths Australia
- Year 2 Maths Australia
- Year 3 Maths Australia
- Year 4 Maths Australia
- Year 5 Maths Australia
- Meet the Sallies
- Certificates
Pythagoras Theorem Questions
Welcome to our Pythagoras' Theorem Questions area. Here you will find help, support and questions to help you master Pythagoras' Theorem and apply it.
For full functionality of this site it is necessary to enable JavaScript.
Here are the instructions how to enable JavaScript in your web browser .
Pythagoras' Theorem Questions
Here you will find our support page to help you learn to use and apply Pythagoras' theorem.
Please note: Pythagoras' Theorem is also called the Pythagorean Theorem
There are a range of sheets involving finding missing sides of right triangles, testing right triangles and solving word problems using Pythagoras' theorem.
Using these sheets will help your child to:
- learn Pythagoras' right triangle theorem;
- use and apply the theorem in a range of contexts to solve problems.
Pythagoras' Theorem
|
| where a,b and c are the sides of a right triangle. |
Pythagoras' Theorem - in more detail
Pythagoras' theorem states that in a right triangle (or right-angled triangle) the sum of the squares of the two smaller sides of the triangle is equal to the square of the hypotenuse.
In other words, \[ a^2 + b^2 = c^2 \]
where c is the hypotenuse (the longest side) and a and b are the other sides of the right triangle.
What does this mean?
This means that for any right triangle, the orange square (which is the square made using the longest side) has the same area as the other two blue squares added together.
Other formulas that can be deduced from the Pythagorean theorem
As a result of the formula \[ a^2 + b^2 = c^2 \] we can also deduce that:
- \[ b^2 = c^2 - a^2 \]
- \[ a^2 = c^2 - b^2 \]
- \[ c = \sqrt{a^2 + b^2} \]
- \[ b = \sqrt {c^2 - a^2} \]
- \[ a = \sqrt {c^2 - b^2} \]
Pythagarean Theorem Examples
Example 1) find the length of the missing side..
In this example, we need to find the hypotenuse (longest side of a right triangle).
So using pythagoras, the sum of the two smaller squares is equal to the square of the hypotenuse.
This gives us \[ 4^2 + 6^2 = ?^2 \]
So \[ ?^2 = 16 + 36 = 52 \]
This gives us \[ ? = \sqrt {52} = 7.21 \; cm \; to \; 2 \; decimal \; places \]
Example 2) Find the length of the missing side.
In this example, we need to find the length of the base of the triangle, given the other two sides.
This gives us \[ ?^2 + 5^2 = 8^2 \]
So \[ ?^2 = 8^2 - 5^2 = 64 - 25 = 39 \]
This gives us \[ ? = \sqrt {39} = 6.25 \; cm \; to \; 2 \; decimal \; places \]
Pythagoras' Theorem Question Worksheets
The following questions involve using Pythagoras' theorem to find the missing side of a right triangle.
The first sheet involves finding the hypotenuse only.
A range of different measurement units have been used in the triangles, which are not drawn to scale.
- Pythagoras Questions Sheet 1
- PDF version
- Pythagoras Questions Sheet 2
- Pythagoras Questions Sheet 3
- Pythagoras Questions Sheet 4
Pythagoras' Theorem Questions - Testing Right Triangles
The following questions involve using Pythagoras' theorem to find out whether or not a triangle is a right triangle, (whether the triangle has a right angle).
If Pythagoras' theorem is true for the triangle, and c 2 = a 2 + b 2 then the triangle is a right triangle.
If Pythagoras' theorem is false for the triangle, and c 2 = a 2 + b 2 then the triangle is not a right triangle.
- Pythagoras Triangle Test Sheet 1
- Pythagoras Triangle Test Sheet 2
Pythagoras' Theorem Questions - Word Problems
The following questions involve using Pythagoras' theorem to solve a range of word problems involving 'real-life' type questions.
On the first sheet, only the hypotenuse needs to be found, given the measurements of the other sides.
Illustrations have been provided to support students solving these word problems.
- Pythagoras Theorem Word Problems 1
- Pythagoras Theorem Word Problems 2
Geometry Formulas
- Geometry Formula Sheet
Here you will find a support page packed with a range of geometric formula.
Included in this page are formula for:
- areas and volumes of 2d and 3d shapes
- interior angles of polygons
- angles of 2d shapes
- triangle formulas and theorems
This page will provide a useful reference for anyone needing a geometric formula.
Triangle Formulas
Here you will find a support page to help you understand some of the special features that triangles have, particularly right triangles.
Using this support page will help you to:
- understand the different types and properties of triangles;
- understand how to find the area of a triangle;
- know and use Pythagoras' Theorem.
All the free printable geometry worksheets in this section support the Elementary Math Benchmarks.
- Geometry Formulas Triangles
Here you will find a range of geometry cheat sheets to help you answer a range of geometry questions.
The sheets contain information about angles, types and properties of 2d and 3d shapes, and also common formulas associated with 2d and 3d shapes.
Included in this page are:
- images of common 2d and 3d shapes;
- properties of 2d and 3d shapes;
- formulas involving 2d shapes, such as area and perimeter, pythagoras' theorem, trigonometry laws, etc;
- formulas involving 3d shapes about volume and surface area.
Using the sheets in this section will help you understand and answer a range of geometry questions.
How to Print or Save these sheets 🖶
Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!
- How to Print support
Subscribe to Math Salamanders News
Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!
- Newsletter Signup
Return to Geometry Section
Return from Pythagoras Theorem Questions to Math Salamanders Homepage
Math-Salamanders.com
The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.
We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.
New! Comments
TOP OF PAGE
© 2010-2024 Math Salamanders Limited. All Rights Reserved.
- Privacy Policy
- Copyright Policy
Pythagorean Theorem Word Problems
In these lessons, we will be looking at how to solve different types of word problems using the Pythagorean Theorem.
Related Pages Pythagorean Theorem Converse Of Pythagorean Theorem Applications Of Pythagorean Theorem More Geometry Lessons
How To Solve Word Problems Using The Pythagorean Theorem?
- Determine whether the word problem can be modeled by a right triangle.
- Use the Pythagorean Theorem to find the missing side if you are given two sides.
Example: Shane marched 3 m east and 6 m north. How far is he from his starting point?
Solution: First, sketch the scenario. The path taken by Shane forms a right-angled triangle. The distance from the starting point forms the hypotenuse.
Example: The rectangle PQRS represents the floor of a room.
Ivan stands at point A. Calculate the distance of Ivan from a) the corner R of the room b) the corner S of the room
Example: In the following diagram of a circle, O is the centre and the radius is 12 cm. AB and EF are straight lines.
Find the length of EF if the length of OP is 6 cm.
Examples Of Real Life Pythagorean Theorem Word Problems
Problem 1: A 35-foot ladder is leaning against the side of a building and is positioned such that the base of the ladder is 21 feet from the base of the building. How far above the ground is the point where the ladder touches the building?
Problem 2: The main mast of a fishing boat is supported by a sturdy rope that extends from the top of the mast to the deck. If the mast is 20 feet tall and the rope attached to the deck 15 feet away from the base of the mast, how long is the rope?
Problem 3: If an equilateral triangle has a height of 8, find the length of each side.
Problem 4: Two cyclist start from the same location. One cyclist travels due north and the other due east, at the same speed. Find the speed of each in miles per hour if after two hours they are 17sqrt(2) miles apart.
Problem 5: Two cars start from the same intersection with one traveling southbound while the other travels eastbound going 10 mph faster. If after two hours they are 10sqrt(34) apart, how fast was each car traveling?
Problem 6: A carpet measures 7 feet long and has a diagonal measurement of sqrt(74) feet. Find the width of the carpet.
Problem 7: Jim and Eileen decided to take a short cut through the woods to go to their friend’s house. When they went home they decided to take the long way around the woods to avoid getting muddy shoes. What total distance did they walk to and from their friend’s house? Dimensions are in meters.
Problem 8: Shari went to a level field to fly a kite. She let out all 650 feet of the string and tied it to a stake. Then, she walked out on the field until she was directly under the kite, which was 600 feet from the stake. How high was the kite from the ground?
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Pythagorean Theorem
The pythagorean theorem.
If we have a right triangle, and we construct squares using the edges or sides of the right triangle (gray triangle in the middle), the area of the largest square built on the hypotenuse (the longest side) is equal to the sum of the areas of the squares built on the other two sides. This is the Pythagorean Theorem in a nutshell. By the way, this is also known as the Pythagoras’ Theorem .
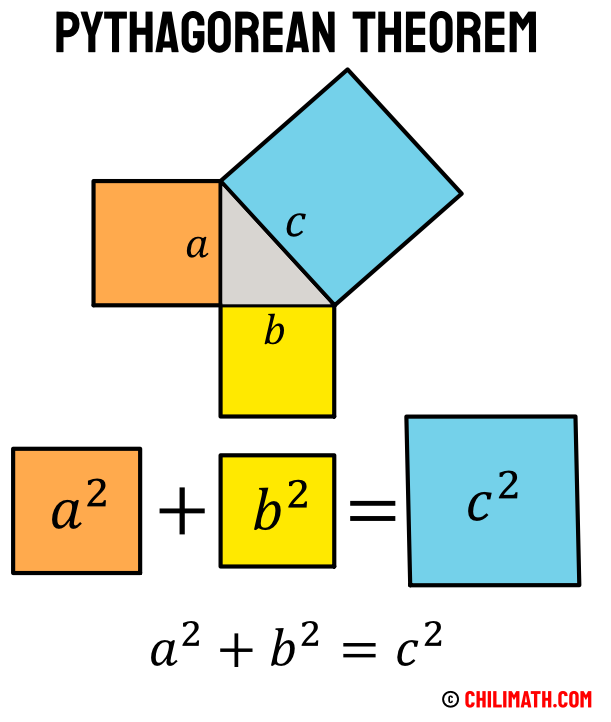
Notice that we square (raised to the second power) the variables [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] to indicate areas. The sum of the smaller squares (orange and yellow) is equal to the largest square (blue).
The Pythagorean Theorem relates the three sides in a right triangle. To be specific, relating the two legs and the hypotenuse, the longest side.
The Pythagorean Theorem can be summarized in a short and compact equation as shown below.
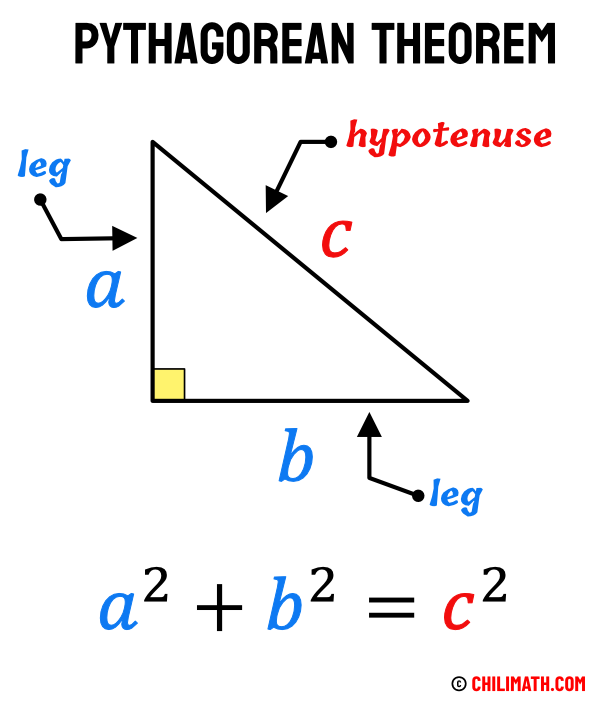
Definition of Pythagorean Theorem
For a given right triangle, it states that the square of the hypotenuse, [latex]c[/latex], is equal to the sum of the squares of the legs, [latex]a[/latex] and [latex]b[/latex]. That is, [latex]{a^2} + {b^2} = {c^2}[/latex].
For a more general definition, we have:
In right a triangle, the square of longest side known as the hypotenuse is equal to the sum of the squares of the other two sides.
The Pythagorean Theorem guarantees that if we know the lengths of two sides of a right triangle, we can always determine the length of the third side.
Here are the three variations of the Pythagorean Theorem formulas:
Let’s go over some examples!
Examples of Applying the Pythagorean Theorem
Example 1: Find the length of the hypotenuse.
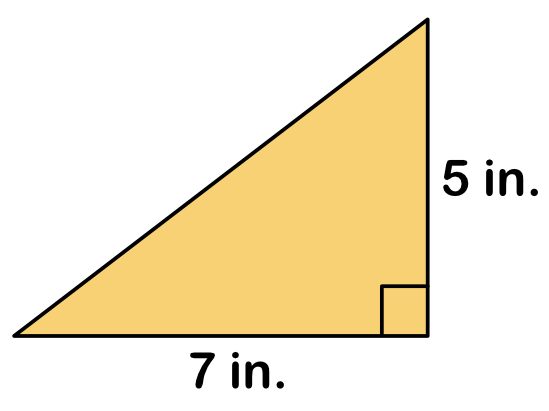
Our goal is to solve for the length of the hypotenuse. We are given the lengths of the two legs. We know two sides out of the three! This is enough information for the formula to work.
For the legs, it doesn’t matter which one we assign for [latex]a[/latex] or [latex]b[/latex]. The result will be the same. So if we let [latex]a=5[/latex], then [latex]b=7[/latex]. Substituting these values into the Pythagorean Formula equation, we get
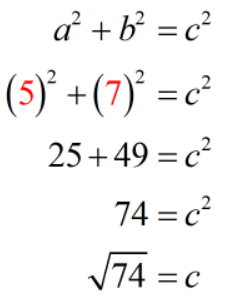
To isolate the variable [latex]c[/latex], we take the square roots of both sides of the equation. That eliminates the square (power of 2) on the right side. And on the left, we simply have a square root of a number which is no big deal.
However, we need to be mindful here when we take the square root of a number. We want to consider only the principal square root or the positive square root since we are dealing with length. It doesn’t make any sense to have a negative length, thus we disregard the negative length!
Therefore, the length of the hypotenuse is [latex]\sqrt {74}[/latex] inches. If we wish to approximate it to the nearest tenth, we have [latex]8.6[/latex] inches.
Example 2: Find the length of the leg.
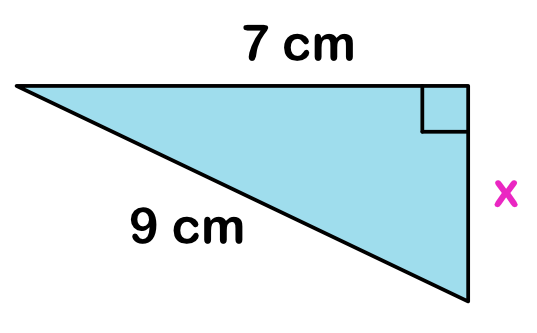
Just by looking at the figure above, we know that we have enough information to solve for the missing side. The reason is the measure of the two sides are given and the other leg is left as unknown. That’s two sides given out of the possible three.
Here, we can let [latex]a[/latex] or [latex]b[/latex] equal [latex]7[/latex]. It really doesn’t matter. So, for this, we let [latex]a=7[/latex]. That means we are solving for the leg [latex]b[/latex]. But for the hypotenuse, there’s no room for error. We have to be certain that we are assigning [latex]c[/latex] for the length, that is, for the longest side. In this case, the longest side has a measure of [latex]9[/latex] cm and that is the value we will assign for [latex]c[/latex], therefore [latex]c=9[/latex].
Let’s calculate the length of leg [latex]b[/latex]. We have [latex]a=7[/latex] and [latex]c=9[/latex].
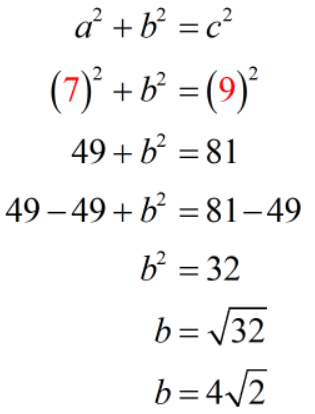
Therefore, the length of the missing leg is [latex]4\sqrt 2[/latex] cm. Rounding it to two decimal places, we have [latex]5.66[/latex] cm.
Example 3: Do the sides [latex]17[/latex], [latex]15[/latex] and [latex]8[/latex] form a right triangle? If so, which sides are the legs and the hypotenuse?
If these are the sides of a right triangle then it must satisfy the Pythagorean Theorem. The sum of the squares of the shorter sides must be equal to the square to the longest side. Obviously, the sides [latex]8[/latex] and [latex]15[/latex] are shorter than [latex]17[/latex] so we will assume that they are the legs and [latex]17[/latex] is the hypotenuse. So we let [latex]a=8[/latex], [latex]b=15[/latex], and [latex]c=17[/latex].
Let’s plug these values into the Pythagorean equation and check if the equation is true.
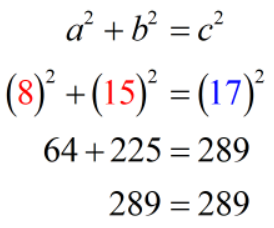
Since we have a true statement, then we have a case of a right triangle! We can now say for sure that the shorter sides [latex]8[/latex] and [latex]15[/latex] are the legs of the right triangle while the longest side [latex]17[/latex] is the hypotenuse.
Example 4: A rectangle has a length of [latex]8[/latex] meters and a width of [latex]6[/latex] meters. What is the length of the diagonal of the rectangle?
The diagonal of a rectangle is just the line segment that connects two non-adjacent vertices. In the figure below, it is obvious that the diagonal is the hypotenuse of the right triangle while the two other sides are the legs which are [latex]8[/latex] and [latex]6[/latex].
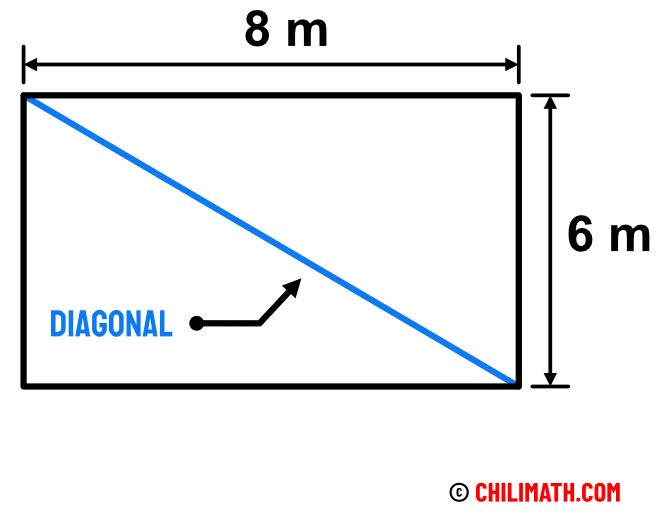
If we let [latex]a=6[/latex] and [latex]b=8[/latex], we can solve for [latex]c[/latex] in the Pythagorean equation which is just the diagonal.
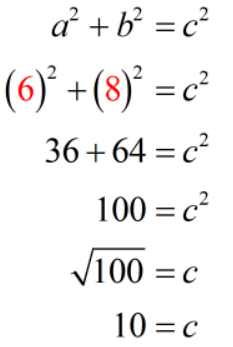
Therefore, the measure of the diagonal is [latex]10[/latex] meters.
Example 5: A ladder is leaning against a wall. The distance from the top of the ladder to the ground is [latex]20[/latex] feet. If the base of the ladder is [latex]4[/latex] feet away from the wall, how long is the ladder?
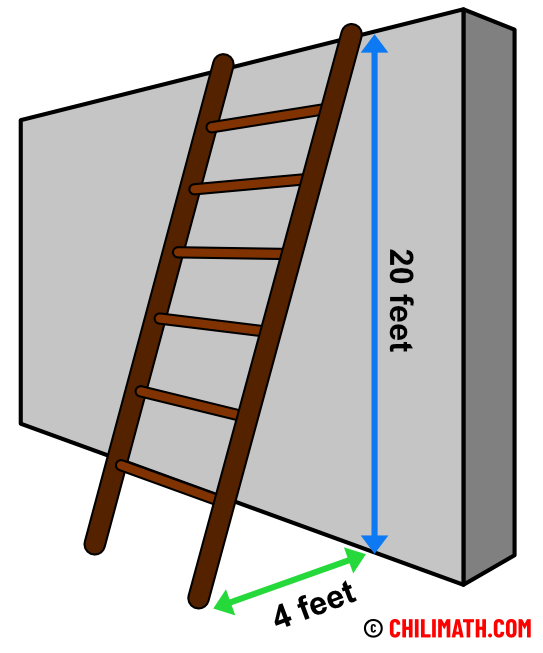
If you study the illustration, the length of the ladder is just the hypotenuse of the right triangle with legs [latex]20[/latex] feet and [latex]4[/latex] feet.
Again, we just need to perform direct substitution into the Pythagorean Theorem formula using the known values then solve for [latex]c[/latex] or the hypotenuse.
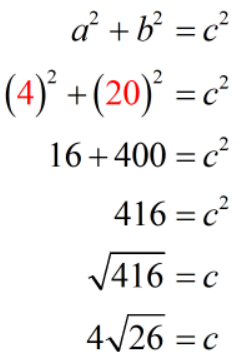
Therefore, the length of the ladder is [latex]4\sqrt {26}[/latex] feet or approximately [latex]20.4[/latex] feet.
Example 6: In a right isosceles triangle, the hypotenuse measures [latex]12[/latex] feet. What is the length of each leg?
Remember that a right isosceles triangle is a triangle that contains a 90-degree angle and two of its sides are congruent.
In the figure below, the hypotenuse is [latex]12[/latex] feet. The two legs are both labeled as [latex]x[/latex] since they are congruent.
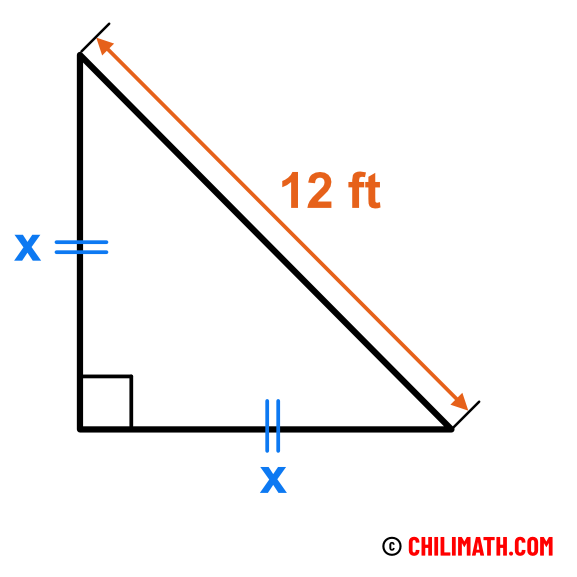
Let’s substitute these values into the formula then solve for the value of [latex]x[/latex]. We know that [latex]x[/latex] is just the leg of the right isosceles triangle which is the unknown that we are trying to solve for.
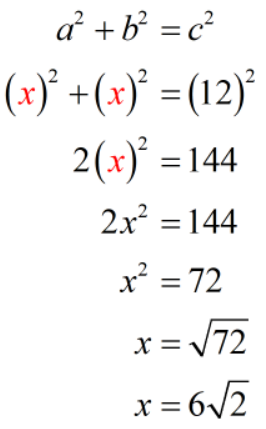
Therefore, the leg of the right isosceles triangle is [latex]6\sqrt 2[/latex] feet. If we want an approximate value, it is [latex]8.49[/latex] feet, rounded to the nearest hundredth.
Example 7: The diagonal of the square below is [latex]2\sqrt 2[/latex]. Find its area.
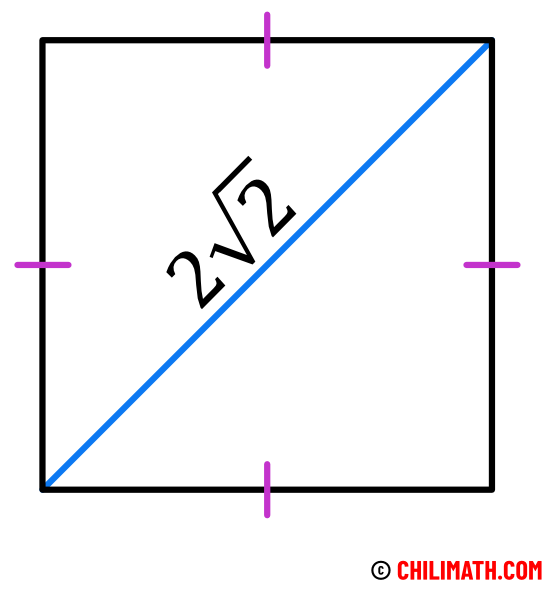
We know the area of the square is given by the formula [latex]A=s^2[/latex] where [latex]s[/latex] is the side of the square. So that means we need to find the side of the square given its diagonal. If we look closely, the diagonal is simply the hypotenuse of a right triangle. More importantly, the legs of the right triangle are also congruent.
Since the legs are congruent, we can let it equal to [latex]x[/latex].
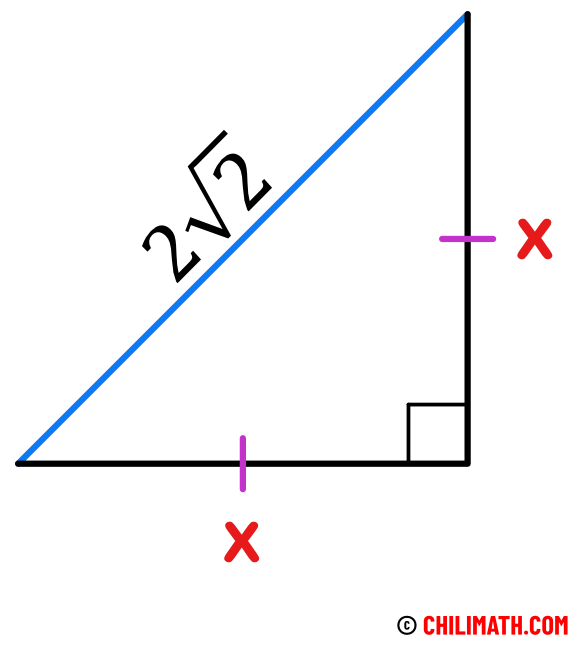
Substitute these values into the Pythagorean Theorem formula then solve for [latex]x[/latex].
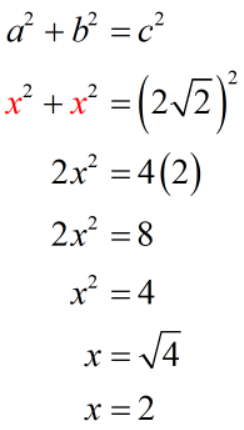
We calculated the length of the leg to be [latex]2[/latex] units. It is also the side of the square. So to find the area of the square, we use the formula
[latex]A = {s^2}[/latex]
That means, the area is
[latex]A = {s^2} = {\left( 2 \right)^2} = 4[/latex]
Therefore, the area of the square is [latex]4[/latex] square units.
You might also like these tutorials:
- Pythagorean Theorem Practice Problems with Answers
- Pythagorean Triples
- Generating Pythagorean Triples
Pythagorean Theorem and Problems with Solutions
Explore some simple proofs of the Pythagorean theorem and its converse and use them to solve problems. Detailed solutions to the problems are also presented.
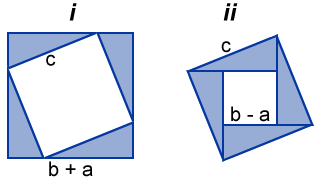
| | In the figure below are shown two squares whose sides are a + b and c. let us write that the area of the large square is the area of the small square plus the total area of all 4 congruent right triangles in the corners of the large square. We first start with a right triangle and then complete it to make a rectangle as shown in the figure below which in turn in made up of three triangles.
Use the Pythagorean to write We use the Pythagorean theorem on triangle CHB (or CHA) to write |
MathBootCamps
The pythagorean theorem with examples.
The Pythagorean theorem is a way of relating the leg lengths of a right triangle to the length of the hypotenuse, which is the side opposite the right angle. Even though it is written in these terms, it can be used to find any of the side as long as you know the lengths of the other two sides. In this lesson, we will look at several different types of examples of applying this theorem.
Table of Contents
- Examples of using the Pythagorean theorem
- Solving applied problems (word problems)
- Solving algebraic problems
[adsenseWide]
Applying the Pythagorean theorem (examples)
In the examples below, we will see how to apply this rule to find any side of a right triangle triangle. As in the formula below, we will let a and b be the lengths of the legs and c be the length of the hypotenuse. Remember though, that you could use any variables to represent these lengths.
In each example, pay close attention to the information given and what we are trying to find. This helps you determine the correct values to use in the different parts of the formula.
Find the value of \(x\).
The side opposite the right angle is the side labelled \(x\). This is the hypotenuse. When applying the Pythagorean theorem, this squared is equal to the sum of the other two sides squared. Mathematically, this means:
\(6^2 + 8^2 = x^2\)
Which is the same as:
\(100 = x^2\)
Therefore, we can write:
\(\begin{align}x &= \sqrt{100}\\ &= \bbox[border: 1px solid black; padding: 2px]{10}\end{align}\)
Maybe you remember that in an equation like this, \(x\) could also be –10, since –10 squared is also 100. But, the length of any side of a triangle can never be negative and therefore we only consider the positive square root.
In other situations, you will be trying to find the length of one of the legs of a right triangle. You can still use the Pythagorean theorem in these types of problems, but you will need to be careful about the order you use the values in the formula.
Find the value of \(y\).
The side opposite the right angle has a length of 12. Therefore, we will write:
\(8^2 + y^2 = 12^2\)
This is the same as:
\(64 + y^2 = 144\)
Subtracting 64 from both sides:
\(y^2 = 80\)
\(\begin{align}y &= \sqrt{80} \\ &= \sqrt{16 \times 5} \\ &= \bbox[border: 1px solid black; padding: 2px]{4\sqrt{5}}\end{align}\)
In this last example, we left the answer in exact form instead of finding a decimal approximation. This is common unless you are working on an applied problem.
Applications (word problems) with the Pythagorean theorem
There are many different kinds of real-life problems that can be solved using the Pythagorean theorem. The easiest way to see that you should be applying this theorem is by drawing a picture of whatever situation is described.
Two hikers leave a cabin at the same time, one heading due south and the other headed due west. After one hour, the hiker walking south has covered 2.8 miles and the hiker walking west has covered 3.1 miles. At that moment, what is the shortest distance between the two hikers?
First, sketch a picture of the information given. Label any unknown value with a variable name, like x.
Due south and due west form a right angle, and the shortest distance between any two points is a straight line. Therefore, we can apply the Pythagorean theorem and write:
\(3.1^2 + 2.8^2 = x^2\)
Here, you will need to use a calculator to simplify the left-hand side:
\(17.45 = x^2\)
Now use your calculator to take the square root. You will likely need to round your answer.
\(\begin{align}x &= \sqrt{17.45} \\ &\approx 4.18 \text{ miles}\end{align}\)
As you can see, it will be up to you to determine that a right angle is part of the situation given in the word problem. If it isn’t, then you can’t use the Pythagorean theorem.
Algebra style problems with the Pythagorean theorem
There is one last type of problem you might run into where you use the Pythagorean theorem to write some type of algebraic expression. This is something that you will not need to do in every course, but it does come up.
A right triangle has a hypotenuse of length \(2x\), a leg of length \(x\), and a leg of length y. Write an expression that shows the value of \(y\) in terms of \(x\).
Since no figure was given, your first step should be to draw one. The order of the legs isn’t important, but remember that the hypotenuse is opposite the right angle.
Now you can apply the Pythagorean theorem to write:
\(x^2 + y^2 = (2x)^2\)
Squaring the right-hand side:
\(x^2 + y^2 = 4x^2\)
When the problem says “the value of \(y\)”, it means you must solve for \(y\). Therefore, we will write:
\(y^2 = 4x^2 – x^2\)
Combining like terms:
\(y^2 = 3x^2\)
Now, use the square root to write:
\(y = \sqrt{3x^2}\)
Finally, this simplifies to give us the expression we are looking for:
\(y = \bbox[border: 1px solid black; padding: 2px]{x\sqrt{3x}}\)
[adsenseLargeRectangle]
The Pythagorean theorem allows you to find the length of any of the three sides of a right triangle. It is one of those things that you should memorize, as it comes up in all areas of math, and therefore in many different math courses you will probably take. Remember to avoid the common mistake of mixing up where the legs go in the formula vs. the hypotenuse and to always draw a picture when one isn’t given.
Share this:
- Click to share on Twitter (Opens in new window)
- Click to share on Facebook (Opens in new window)
- Maths Questions
Pythagoras Theorem Questions
Pythagoras theorem questions with detailed solutions are given for students to practice and understand the concept. Practising these questions will be a plus point in preparation for examinations. Let us discuss in brief about the Pythagoras theorem.
Pythagoras’ theorem is all about the relation between sides of a right-angled triangle. According to the theorem, the hypotenuse square equals the sum of squares of the perpendicular sides.
| = (Perpendicular) + (Base) |
Click here to learn the proof of Pythagoras’ Theorem .
Video Lesson on Pythagoras Theorem
Pythagoras Theorem Questions with Solutions
Now that we have learnt about the Pythagoras Theorem, lets apply the same by solving the following questions.
Question 1: In a right-angled triangle, the measures of the perpendicular sides are 6 cm and 11 cm. Find the length of the third side.
Let ΔABC be the triangle, right-angled at B, such that AB and BC are the perpendicular sides. Let AB = 6 cm and BC = 11 cm
Then, by the Pythagoras theorem,
AC 2 = AB 2 + BC 2
\(\begin{array}{l}\Rightarrow AC=\sqrt{(AB^{2}+BC^{2})}=\sqrt{6^{2}+11^{2}}\end{array} \)
\(\begin{array}{l}=\sqrt{36+121}=\sqrt{157}\end{array} \)
∴ AC = √157 cm.
Question 2: A triangle is given whose sides are of length 21 cm, 20 cm and 29 cm. Check whether these are the sides of a right-angled triangle.
If these are the sides of a right-angled triangle, it must satisfy the Pythagoras theorem.
We have to check whether 21 2 + 20 2 = 29 2
Now, 21 2 + 20 2 = 441 + 400 = 841 = 29 2
Thus, the given triangle is a right-angled triangle.
|
If three integers a, b and c are such that a + b = c , then (a, b, c) is called Pythagorean triples.
For any given integer m, (m – 1, 2m, m + 1) is the Pythagorean triplet. Learn more about . |
Question 3: Find the Pythagorean triplet with whose one number is 6.
Now, m 2 + 1 = 9 + 1 = 10
and m 2 – 1 = 9 – 1 = 8
Therefore, the Pythagorean triplet is (6, 8, 10).
Question 4: The length of the diagonal of a square is 6 cm. Find the sides of the square.
Let ABCD be the square, and let AC be the diagonal of length 6 cm. Then triangle ABC is the right-angled triangle such that AB = BC (∵ all sides of a square are equal)
By Pythagoras theorem,
⇒ AC 2 = 2AB 2
⇒ AC = √2 AB
⇒ AB = (1/√2) AC = (1/√2)6 = 3√2 cm.
Question 5: A ladder is kept at a distance of 15 cm from the wall such that the top of the ladder is at the height of 8 cm from the bottom of the wall. Find the length of the wall.
Let AB be the ladder of length x.
AC 2 + BC 2 = AB 2
\(\begin{array}{l}\Rightarrow AB=\sqrt{AC^{2}+BC^{2}}\end{array} \)
\(\begin{array}{l}\Rightarrow x=\sqrt{8^{2}+15^{2}}=\sqrt{64+225}\end{array} \)
⇒ x = 17 cm
∴ Length of the ladder is 17 cm.
Question 6: Find the area of a rectangle whose length is 144 cm and the length of the diagonal 145 cm.
Let the rectangle be ABCD
\(\begin{array}{l}\Rightarrow AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{145^{2}-144^{2)}\end{array} \)
⇒ AD = √(21025 – 20736) = √289
⇒ AD = 17 cm
Thus, area of the rectangle ABCD = 17 × 144 = 2448 cm 2 .
- Properties of Triangles
- Congruence of Triangles
- Similar Triangles
- Trigonometry
Question 7: A boy travels 24 km towards east from his house, then he turned his left and covers another 10 km. Find out his total displacement?
Let the boy’s house is at point O, then to find the total displacement, we have to find OB.
Clearly, ΔOAB is a right-angled triangle, by Pythagoras theorem,
\(\begin{array}{l} OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{24^{2}-10^{2}}\end{array} \)
⇒ OB = √(576 + 100) = √676
⇒ OB = 26 km.
Question 8: Find the distance between a tower and a building of height 65 m and 34 m, respectively, such that the distance between their top is 29 m.
The figure below shows the situation. Let x be the distance between the tower and the building.
In right triangle DCE, by Pythagoras theorem,
CE = √(DE 2 – DC 2 ) = √(29 2 – 21 2 )
⇒ x = √(841 – 441) = √400
⇒ x = 20 m.
∴ the distance between the tower and the building is 20 m.
Question 9: Find the area of the triangle formed by the chord of length 10 cm of the circle whose radius is 13 cm.
Let AB be the chord of the circle with the centre at O such that AB = 10 and OA = OB = 13. Draw a perpendicular OM on AB.
By the property of circle, perpendicular dropped from the centre of the circle on a chord, bisects the chord.
Then, AM = MB = 5 cm.
Now, in right triangle OMB,
OB 2 = OM 2 + MB 2
⇒ OM = √(OB 2 – MB 2 )
⇒ OM = √(13 2 – 5 2 ) = √(169 – 25)
⇒ OM = √144 = 12 cm
Area of triangle OAB = ½ × AB × OM
= ½ × 10 × 12
= 60 cm 2 .
Question 10: Find the length of tangent PT where P is a point which is at a distance 10 cm from the centre O of the circle of radius 6 cm.
Given, OP = 10 cm and OT = 6m.
We have to find the value of PT.
By the property of tangents, the radius of the circle is perpendicular to the tangent at the point of contact.
Thus, triangle OTP is a right-angled triangle.
∴ by the Pythagoras theorem,
OP 2 = OT 2. + PT 2
⇒ PT = √(OP 2 – OT 2 ) = √(10 2 – 6 2 )
⇒ PT = √(100 – 36) = √64
⇒ PT = 8 cm.
Related Video on Pythagorean Triples
|
|
|
|
|
|
Practice Questions on Pythagoras Theorem
1. Find the area of a right-angled triangle whose hypotenuse is 13 cm and one of the perpendicular sides is 5 cm.
2. Find the Pythagorean triplet whose one member is 15.
3. Find the perimeter of a rectangle whose diagonal is 5 cm and one of its sides is 4 cm.
4 if a pole of length 65 cm is kept leaning against a wall such that the pole reaches up to a height of 63 cm on the wall from the ground. Find the distance between the pole and the wall.
5. Find the area of the triangle inscribed within a circle of radius 8.5 cm such that one of the sides of the triangle is the diameter of the circle and the length of the other side is 8 cm.
(Hint: The triangle is formed in semi-circular region and angle of a semi-circle is of 90 o )
Learn about various mathematical concepts in a simple manner with detailed information, along with step by step solutions to all questions, only at BYJU’S. Download BYJU’S – The Learning App to get personalised videos.
| MATHS Related Links | |
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Pythagorean Theorem
This is generalized by the Pythagorean Inequality and the Law of Cosines .
- 1.1 Proof 1
- 1.2 Proof 2
- 1.3 Proof 3
- 2 Common Pythagorean Triples
- 3.1 Introductory
- 3.2.1 Solution 1 (Bash)
- 3.2.2 Solution 2 (Using 3-4-5)
- 3.3.1 Solution (Casework)
- 4 External links
Common Pythagorean Triples
Also, if (a,b,c) are a pythagorean triplet it follows that (ka,kb,kc) will also form a pythagorean triplet for any constant k.
k can also be imaginary.
Introductory
- 2006 AIME I Problem 1
- 2007 AMC 12A Problem 10
Sample Problem
Solution 1 (Bash)
Solution 2 (Using 3-4-5)
Another Problem
Solution (Casework)
3 and 4 are the legs. Then 5 is the hypotenuse.
3 is a leg and 4 is the hypotenuse.
There are no more cases as the hypotenuse has to be greater than the leg.
External links
- 122 proofs of the Pythagorean Theorem
Something appears to not have loaded correctly.
Click to refresh .
Module 11: Geometry
Using the pythagorean theorem to solve problems, learning outcomes.
- Use the pythagorean theorem to find the unknown length of a right triangle given the two other lengths
The Pythagorean Theorem is a special property of right triangles that has been used since ancient times. It is named after the Greek philosopher and mathematician Pythagoras who lived around [latex]500[/latex] BCE.
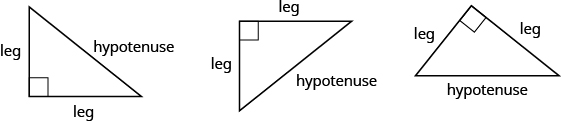
Remember that a right triangle has a [latex]90^\circ [/latex] angle, which we usually mark with a small square in the corner. The side of the triangle opposite the [latex]90^\circ [/latex] angle is called the hypotenuse, and the other two sides are called the legs. See the triangles below.
In a right triangle, the side opposite the [latex]90^\circ [/latex] angle is called the hypotenuse and each of the other sides is called a leg.
The Pythagorean Theorem
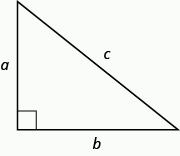
In any right triangle [latex]\Delta ABC[/latex],
[latex]{a}^{2}+{b}^{2}={c}^{2}[/latex]
where [latex]c[/latex] is the length of the hypotenuse [latex]a[/latex] and [latex]b[/latex] are the lengths of the legs.
To solve problems that use the Pythagorean Theorem, we will need to find square roots. In Simplify and Use Square Roots we introduced the notation [latex]\sqrt{m}[/latex] and defined it in this way:
[latex]\text{If }m={n}^{2},\text{ then }\sqrt{m}=n\text{ for }n\ge 0[/latex]
For example, we found that [latex]\sqrt{25}[/latex] is [latex]5[/latex] because [latex]{5}^{2}=25[/latex].
We will use this definition of square roots to solve for the length of a side in a right triangle.
Use the Pythagorean Theorem to find the length of the hypotenuse.
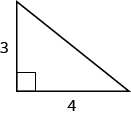
| Step 1. the problem. | |
| Step 2. what you are looking for. | the length of the hypotenuse of the triangle |
| Step 3. Choose a variable to represent it. | Let [latex]c=\text{the length of the hypotenuse}[/latex]
|
| Step 4. Write the appropriate formula. Substitute. | [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex] [latex]{3}^{2}+{4}^{2}={c}^{2}[/latex] |
| Step 5. the equation. | [latex]9+16={c}^{2}[/latex] [latex]25={c}^{2}[/latex] [latex]\sqrt{25}={c}^{2}[/latex] [latex]5=c[/latex] |
| Step 6.
| [latex]{3}^{2}+{4}^{2}=\color{red}{{5}^{2}}[/latex] [latex]9+16\stackrel{?}{=}25[/latex] [latex]25+25\checkmark[/latex] |
| Step 7. the question. | The length of the hypotenuse is [latex]5[/latex]. |
Use the Pythagorean Theorem to find the length of the longer leg.
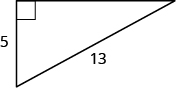
| Step 1. the problem. | |
| Step 2. what you are looking for. | The length of the leg of the triangle |
| Step 3. Choose a variable to represent it. | Let [latex]b=\text{the leg of the triangle}[/latex] Label side
|
| Step 4. Write the appropriate formula. Substitute. | [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex] [latex]{5}^{2}+{b}^{2}={13}^{2}[/latex] |
| Step 5. the equation. Isolate the variable term. Use the definition of the square root. Simplify. | [latex]25+{b}^{2}=169[/latex] [latex]{b}^{2}=144[/latex] [latex]{b}^{2}=\sqrt{144}[/latex] [latex]b=12[/latex] |
| Step 6. [latex]{5}^{2}+\color{red}{12}^{2}\stackrel{?}{=}{13}^{2}[/latex] [latex]25+144\stackrel{?}{=}169[/latex] [latex]169=169\checkmark[/latex] | |
| Step 7. the question. | The length of the leg is [latex]12[/latex]. |
Kelvin is building a gazebo and wants to brace each corner by placing a [latex]\text{10-inch}[/latex] wooden bracket diagonally as shown. How far below the corner should he fasten the bracket if he wants the distances from the corner to each end of the bracket to be equal? Approximate to the nearest tenth of an inch.
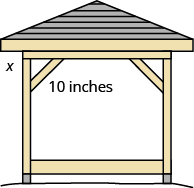
| Step 1. the problem. | |
| Step 2. what you are looking for. | the distance from the corner that the bracket should be attached |
| Step 3. Choose a variable to represent it. | Let = the distance from the corner
|
| Step 4. Write the appropriate formula. Substitute. | [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex] [latex]{x}^{2}+{x}^{2}={10}^{2}[/latex] |
| Step 5. the equation. Isolate the variable. Use the definition of the square root. Simplify. Approximate to the nearest tenth. | [latex]2x^2=100[/latex] [latex]x^2=50[/latex] [latex]x=\sqrt{50}[/latex] [latex]b\approx{7.1}[/latex]
|
| Step 6. [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex] [latex](\color{red}{7.1})^2+(\color{red}{7.1})^{2}\stackrel{\text{?}}{\approx}{10}^{2}[/latex] [latex]50.41+50.41=100.82\approx{100}\quad\checkmark[/latex] Yes. | |
| Step 7. the question. | Kelvin should fasten each piece of wood approximately [latex]7.1″[/latex] from the corner. |
In the following video we show two more examples of how to use the Pythagorean Theorem to solve application problems.
- Question ID 146918, 146916, 146914, 146913. Authored by : Lumen Learning. License : CC BY: Attribution
- Solve Applications Using the Pythagorean Theorem (c only). Authored by : James Sousa (mathispower4u.com). Located at : https://youtu.be/2P0dJxpwFMY . License : CC BY: Attribution
- Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
- High School
- High school geometry
- Pythagorean Theorem
Expert Guidance for Your Pythagorean Theorem Questions
Two congruent circles with centres at (2,3) and (5,6), which intersect at right angles, have radius equal to?
State whether the given statement is true or false: 9, 40, 41 is a Pythagorean triplet. True or false
5, 12, 13 is a Pythagorean triplet. True or false
8, 15, 17 is a Pythagorean triplet
Based on Pythagorean identities, which equation is true? A. sin 2 θ − 1 = cos 2 θ B. sec 2 θ − tan 2 θ = − 1 C. - cos 2 θ − 1 = sin 2 θ D. cot 2 θ − csc 2 θ = − 1
The end rollers of bar AB(1.5R) are constrained to the slot. If roller A has a downward velocity of 1.2 m/s and this speed is constant over a small motion interval, determine the tangential acceleration of roller B as it passes the topmost position. The value of R is 0.5 m.
The area of the obtuse angle triangle shown below is: A17.5 sq. units B 25 sq. units C 14 sq. units D 15 sq. units
Replacing x with 1 2 in 2 x 2 will give you an answer of 1.
Why does the Pythagorean theorem only work for right triangles?
7, 24, 25 is a Pythagorean triplet. A.True B.False
A bicycle wheel with a 5 inch ray rotates 60 ∘ . What distance has the bicycle traveled?
The legs of a right triangle are 6 and 8 cm. Find the hypotenuse and the area of the triangle.
Solve for X. Anlge A=8x+5 Angle B=4 x 2 -10 Angle C= x 2 +2x+10 I know that they equal 180 degrees. However I am drawinga blank on the factoring part of it
For each of the following, can the measures represent sides ofa right triangle? Explain your answers.a. 3 m, 4 m, 5 mb. 2 c m , 3 c m , 5 c m
A 10-m ladder is leaning against a building. The bottom of theladder is 5-m from the building. How high is the top of theladder?
Pythagorean theorem and its cause I'm in high school, and one of my problems with geometry is the Pythagorean theorem. I'm very curious, and everything I learn, I ask "but why?". I've reached a point where I understand what the Pythagorean theorem is, and I understand the equation, but I can't understand why it is that way. Like many things in math, I came to the conclusion that it is that way because it is; math is the laws of the universe, and it may reach a point where the "why" answers itself. So what I want to know is, is there an explication to why the addition of the squared lengths of the smaller sides is equal to the squared hypotenuse, or is it just a characteristic of the right triangle itself? And is math the answer to itself? Thank you.
pythagorean theorem extensions are there for a given integer N solutions to the equations ∑ n = 1 N x i 2 = z 2 for integers x i and zan easier equation given an integer number 'a' can be there solutions to the equation ∑ n = 1 N x i 2 = a 2 for N=2 this is pythagorean theorem
"Pythagorean theorem" for projection onto convex set I'm going through the book on online convex optimization by Hazan, and in the first chapter I saw this assertion (which Hazan calls the "pythagorean theorem"): Let K ⊂ R d be a convex set, y ∈ R d , and x = Π K ( y ) . Then for any z ∈ K we have: ‖ y − z ‖ ≥ ‖ x − z ‖ . It is presented without proof - what is a proof for this? Also, how does it relate to the pythagorean theorem?
Non-geometric Proof of Pythagorean Theorem Is there a purely algebraic proof for the Pythagorean theorem that doesn't rely on a geometric representation? Just algebra/calculus. I want to TRULY understand the WHY of how it is true. I know it works and I know the geometric proofs.
The Pythagorean theorem and Hilbert axioms Can one state and prove the Pythagorean theorem using Hilbert's axioms of geometry, without any reference to arithmetic? Edit: Here is a possible motivation for this question (and in particular for the "state" part of this question). It is known that the theory of Euclidean geometry is complete. Every true statement in this theory is provable. On the other hand, it is known that the axioms of (Peano) arithmetic cannot be proven to be consistent. So, basically, I ask if there is a reasonable theory which is known to be consistent and complete, and in which the Pythagorean theorem can be stated and proved. In summary, I guess I am asking - can we be sure that the Pythagorean theorem is true? :)
- Solid Geometry
- Conic sections
- Analytic geometry
- Transformation properties
- Performing transformations
- Maximization
- Arc of a Circle
- Geometric Probability
- Angle theorems
- Finding volume
- Distance Formula
- Indirect Proof
- Vertices Of An Ellipse
- Quadrilaterals
- Logical Reasoning
- High School Questions
- College Questions
- Math Solver
- Top Questions
- Top Questions 2
- Term of Service
- Payment Policy
Connect with us
Get Plainmath App
- Google Play
E-mail us: [email protected]
Our Service is useful for:
Plainmath is a platform aimed to help users to understand how to solve math problems by providing accumulated knowledge on different topics and accessible examples.
2023 Plainmath. All rights reserved
- Math Forum/Help
- Problem Solver
- College Math
- Pythagorean Theorem
Pythagorean Theorem: Problems with Solutions
Right Triangles
Rules, Formula and more
Pythagorean Theorem
The sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse .
Usually, this theorem is expressed as $$ A^2 + B^2 = C^2 $$ .
Right Triangle Properties
A right triangle has one $$ 90^{\circ} $$ angle ($$ \angle $$ B in the picture on the left) and a variety of often-studied formulas such as:
- The Pythagorean Theorem
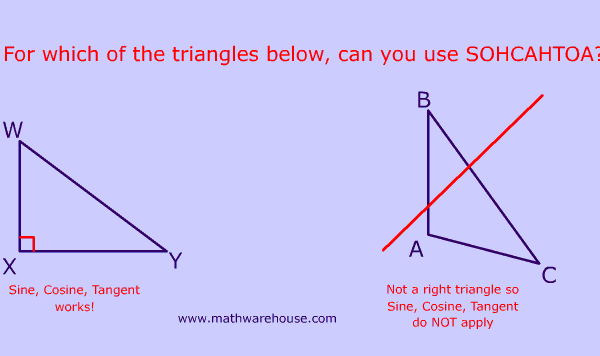
- Trigonometry Ratios (SOHCAHTOA)
- Pythagorean Theorem vs Sohcahtoa (which to use)
SOHCAHTOA only applies to right triangles ( more here ) .
A Right Triangle's Hypotenuse
The hypotenuse is the largest side in a right triangle and is always opposite the right angle.
In the triangle above, the hypotenuse is the side AB which is opposite the right angle, $$ \angle C $$.
Online tool calculates the hypotenuse (or a leg) using the Pythagorean theorem.
Practice Problems
Below are several practice problems involving the Pythagorean theorem, you can also get more detailed lesson on how to use the Pythagorean theorem here .
Find the length of side t in the triangle on the left.
Substitute the two known sides into the Pythagorean theorem's formula : A² + B² = C²
What is the value of x in the picture on the left?
Set up the Pythagorean Theorem : 14 2 + 48 2 = x 2 2,500 = X 2
$$ x = \sqrt{2500} = 50 $$
$$ x^2 = 21^2 + 72^2 \\ x^2= 5625 \\ x = \sqrt{5625} \\ x =75 $$
Find the length of side X in the triangle on on the left?
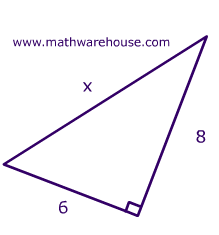
Substitue the two known sides into the pythagorean theorem's formula : $$ A^2 + B^2 = C^2 \\ 8^2 + 6^2 = x^2 \\ x = \sqrt{100}=10 $$
What is x in the triangle on the left?
x 2 + 4 2 = 5 2 x 2 + 16 = 25 x 2 = 25 - 16 = 9 x = 3
Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!
Popular pages @ mathwarehouse.com.
Pythagorean theorem - practice problems
Number of problems found: 1367.
- all math problems 19112
- planimetrics 3462
- Pythagorean theorem 1367
- right triangle 1035
- triangle 904
- expression of a variable from the formula 549
- square root 435
- area of a shape 418
- diagonal 302
- surface area 277
- New math problems
- Popular math problems
- Harder math problems
- The easiest word problems
Pythagorean Theorem Calculator
Please provide any 2 values below to solve the Pythagorean equation: a 2 + b 2 = c 2 .
| a = |
 Related Triangle Calculator | Right Triangle Calculator Pythagorean TheoremThe Pythagorean Theorem, also known as Pythagoras' theorem, is a fundamental relation between the three sides of a right triangle. Given a right triangle, which is a triangle in which one of the angles is 90°, the Pythagorean theorem states that the area of the square formed by the longest side of the right triangle (the hypotenuse) is equal to the sum of the area of the squares formed by the other two sides of the right triangle:  In other words, given that the longest side c = the hypotenuse, and a and b = the other sides of the triangle: a 2 + b 2 = c 2 This is known as the Pythagorean equation, named after the ancient Greek thinker Pythagoras. This relationship is useful because if two sides of a right triangle are known, the Pythagorean theorem can be used to determine the length of the third side. Referencing the above diagram, if a = 3 and b = 4 the length of c can be determined as: c = √ a 2 + b 2 = √ 3 2 +4 2 = √ 25 = 5 It follows that the length of a and b can also be determined if the lengths of the other two sides are known using the following relationships: a = √ c 2 - b 2 b = √ c 2 - a 2 The law of cosines is a generalization of the Pythagorean theorem that can be used to determine the length of any side of a triangle if the lengths and angles of the other two sides of the triangle are known. If the angle between the other sides is a right angle, the law of cosines reduces to the Pythagorean equation. There are a multitude of proofs for the Pythagorean theorem, possibly even the greatest number of any mathematical theorem. Algebraic proof:  In the figure above, there are two orientations of copies of right triangles used to form a smaller and larger square, labeled i and ii, that depict two algebraic proofs of the Pythagorean theorem. In the first one, i, the four copies of the same triangle are arranged around a square with sides c. This results in the formation of a larger square with sides of length b + a, and area of (b + a) 2 . The sum of the area of these four triangles and the smaller square must equal the area of the larger square such that:
| |||||||||||||||||||||||||||||||
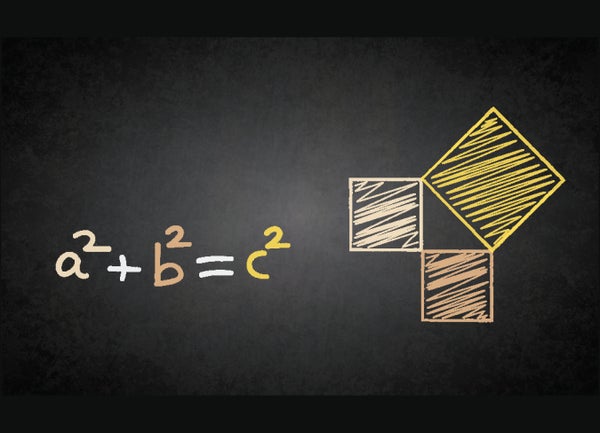
IMAGES
VIDEO
COMMENTS
Here are eight (8) Pythagorean Theorem problems for you to solve. You might need to find either the leg or the hypotenuse of the right triangle. These problems vary in type and difficulty, providing you an opportunity to level up your skills. ... Pythagorean Theorem Practice Problems with Answers. There are eight (8) problems here about the ...
Example 2 (solving for a Leg) Use the Pythagorean theorem to determine the length of X. Step 1. Identify the legs and the hypotenuse of the right triangle. The legs have length 24 and X X are the legs. The hypotenuse is 26. Step 2. Substitute values into the formula (remember 'C' is the hypotenuse). A2 + B2 = C2 x2 + 242 = 262 A 2 + B 2 = C 2 x ...
Word problems using the Pythagorean Theorem: 1. A person has to walk 100 m to go from position X in the north of east direction to the position B and then to the west of Y to reach finally at position Z. The position Z is situated at the north of X and at a distance of 60 m from X. Find the distance between X and Y. Solution:
Pythagorean Theorem in 8th grade. Pythagorean Theorem is usually introduced in middle school, as it is a part of the 8th grade Common Core Math Standards. The emphasis in middle school is on students being able to: Explain the Pythagorean Theorem; Use the theorem to solve mathematical and real-world problems - with both 2D and 3D figures;
How to Solve the Pythagorean Theorem - Example Problems. For example, find the hypotenuse of a right triangle with side that have lengths of 5 and 12. Start with the formula for the Pythagorean theorem and plug in the numbers for the sides a and b to solve for c. a 2 + b 2 = c 2 5 2 + 12 2 = c 2 c 2 = 5 2 + 12 2 = 25 + 144 = 169 c2 = 169 c ...
a) d) 8) A right triangle has legs of 52.6 cm and 35.7 cm. Determine the length of the triangle's hypotenuse. 9) A right triangle has a hypotenuse of 152.6 m. The length of one of the other sides is 89.4 m. Determine the length of the third side. 10) For each of the following, the side lengths of a triangle are given.
Other formulas that can be deduced from the Pythagorean theorem. As a result of the formula \[ a^2 + b^2 = c^2 \] we can also deduce that: \[ b^2 = c^2 - a^2 \] ... The following questions involve using Pythagoras' theorem to solve a range of word problems involving 'real-life' type questions. On the first sheet, only the hypotenuse needs to be ...
Find the length of EF if the length of OP is 6 cm. Solution: OE is the radius of the circle, which is 12 cm. OP 2 + PE 2 = OE 2. 6 2 + PE 2 = 12 2. PE =. EF = 2 × PE = 20.78 cm. Examples Of Real Life Pythagorean Theorem Word Problems. Problem 1: A 35-foot ladder is leaning against the side of a building and is positioned such that the base of ...
The Pythagorean Theorem can be summarized in a short and compact equation as shown below. For a given right triangle, it states that the square of the hypotenuse, In right a triangle, the square of longest side known as the hypotenuse is equal to the sum of the squares of the other two sides. The Pythagorean Theorem guarantees that if we know ...
Click here for Answers. . Practice Questions. Previous: Rotations Practice Questions. Next: Direct and Inverse Proportion Practice Questions. The Corbettmaths Practice Questions on Pythagoras.
Detailed Solutions to the Above Problems. Solution to Problem 1. Given the hypotenuse and one of the sides, we use the Pythagorean theorem to find the second side x as follows. x 2 + 6 2 = 10 2. Solve for x. x = √ (10 2 - 6 2) = 8. Area of the triangle = (1 / 2) height × base.
Solution. The side opposite the right angle is the side labelled \ (x\). This is the hypotenuse. When applying the Pythagorean theorem, this squared is equal to the sum of the other two sides squared. Mathematically, this means: \ (6^2 + 8^2 = x^2\) Which is the same as: \ (100 = x^2\) Therefore, we can write:
Practice Questions on Pythagoras Theorem. 1. Find the area of a right-angled triangle whose hypotenuse is 13 cm and one of the perpendicular sides is 5 cm. 2. Find the Pythagorean triplet whose one member is 15. 3. Find the perimeter of a rectangle whose diagonal is 5 cm and one of its sides is 4 cm.
The Pythagorean Theorem is one of the most frequently used theorems in geometry, and is one of the many tools in a good geometer's arsenal. A very large number of geometry problems can be solved by building right triangles and applying the Pythagorean Theorem. This is generalized by the Pythagorean Inequality and the Law of Cosines .
To solve problems that use the Pythagorean Theorem, we will need to find square roots. In Simplify and Use Square Roots we introduced the notation √m m and defined it in this way: If m= n2, then √m = n for n ≥0 If m = n 2, then m = n for n ≥ 0. For example, we found that √25 25 is 5 5 because 52 =25 5 2 = 25.
kramberol 2022-07-11. pythagorean theorem extensions. are there for a given integer N solutions to the equations. ∑ n = 1 N x i 2 = z 2. for integers x i and zan easier equation given an integer number 'a' can be there solutions to the equation. ∑ n = 1 N x i 2 = a 2. for N=2 this is pythagorean theorem.
Calculate the total area of the plot. Answer: square kilometers. It is given the length of the diagonal of the square. It divides it into two equal triangles. In addition, the two triangles are right and the legs of the same length. be the length of square side and by the Pythagorean theorem we get: \displaystyle x^ {2} +x^ {2}=\left (2\sqrt {2 ...
Discover the Pythagorean theorem and how to apply it to solve problems involving right triangles. Practice with interactive examples and exercises.
A Right Triangle's Hypotenuse. The hypotenuse is the largest side in a right triangle and is always opposite the right angle. (Only right triangles have a hypotenuse). The other two sides of the triangle, AC and CB are referred to as the 'legs'. In the triangle above, the hypotenuse is the side AB which is opposite the right angle, ∠C ∠ C.
Worksheet #1 - Word Problems Pythagorean Theorem Directions: Solve by drawing a picture, identifying a, b, and c, and applying the Pythagorean Theorem. Do not forget to give your answer with units and show ALL your work to receive full credit. 1. Two sides of a right triangle are 8 inches and 12 inches. a.
Pythagorean theorem - practice problems. The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be written as: where c is the length of the hypotenuse, and a and b are the ...
a 2 + b 2 = c 2. This is known as the Pythagorean equation, named after the ancient Greek thinker Pythagoras. This relationship is useful because if two sides of a right triangle are known, the Pythagorean theorem can be used to determine the length of the third side. Referencing the above diagram, if. a = 3 and b = 4.
The Pythagorean theorem provides an equation to calculate the longer side of a right triangle by summing the squares of the other two sides. It is often phrased as a2 + b2 = c2. In this equation ...
Classical Greek brainiac Pythagoras created a theorem that goes like this. The area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas ...